1、幂零矩阵

2、可拆解为A+E型矩阵的运算

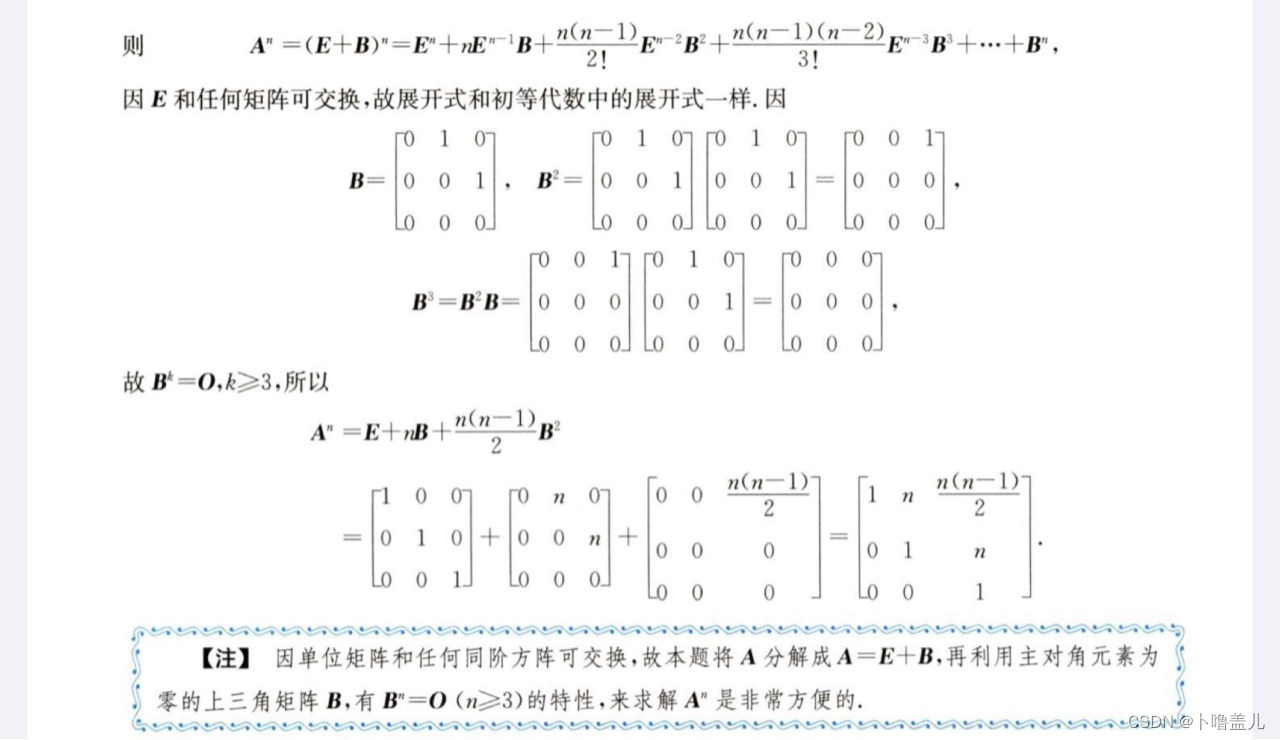
3、正交与施密特化
1️⃣正交

2️⃣施密特正交化
意义:将两个线性无关的向量变成正交单位向量。

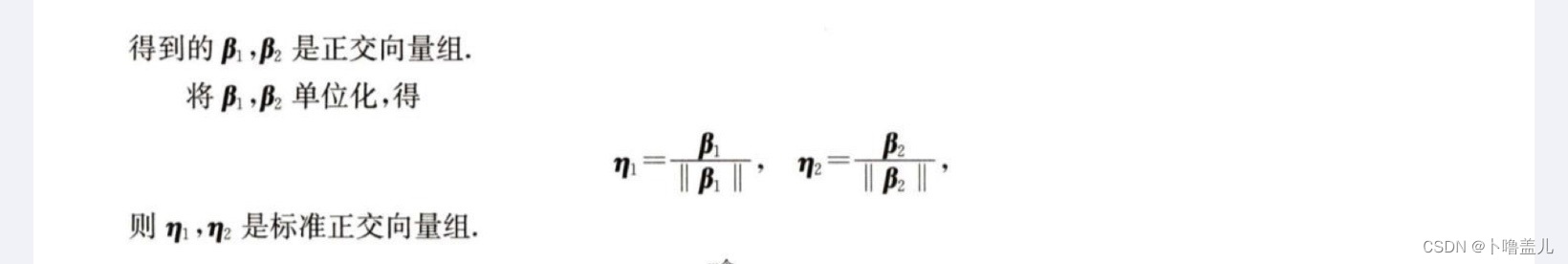
来一道题:
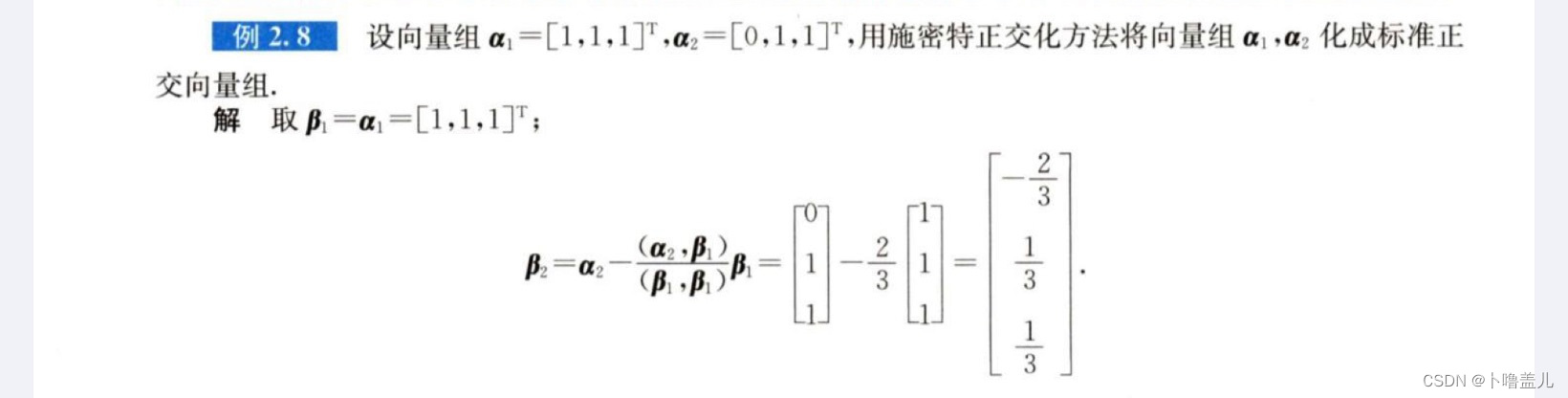

4、 转置+求逆
1️⃣转置运算

2️⃣求逆运算
🔡基本公式A A*=|A|E
🔡A和E拼接、通过初等变换反过来
🔡找到AB=E 的B
🔡将A分解成B·C、A的逆通过简单的BC求
🔡分块矩阵的逆矩阵

5、等价矩阵(已知A和B等价,求全部P)
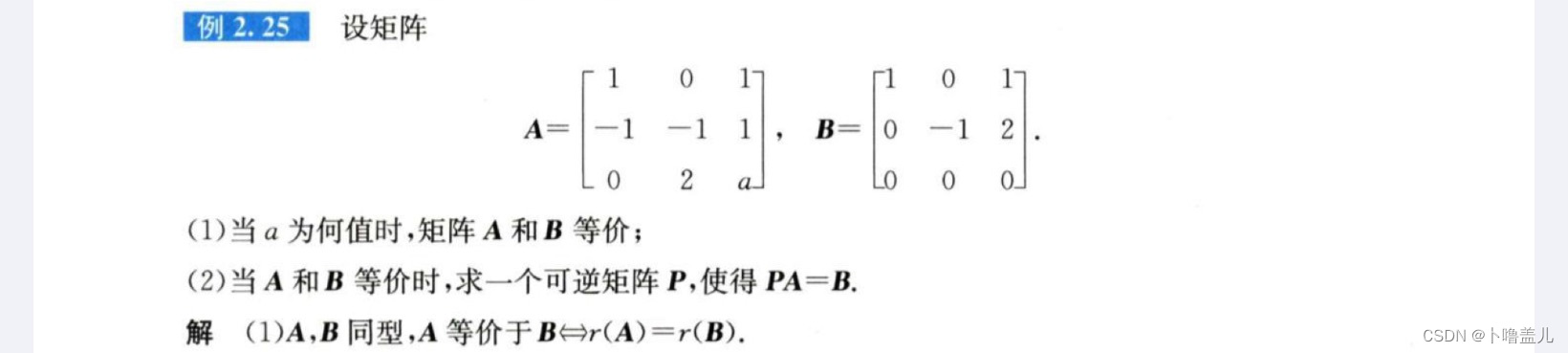
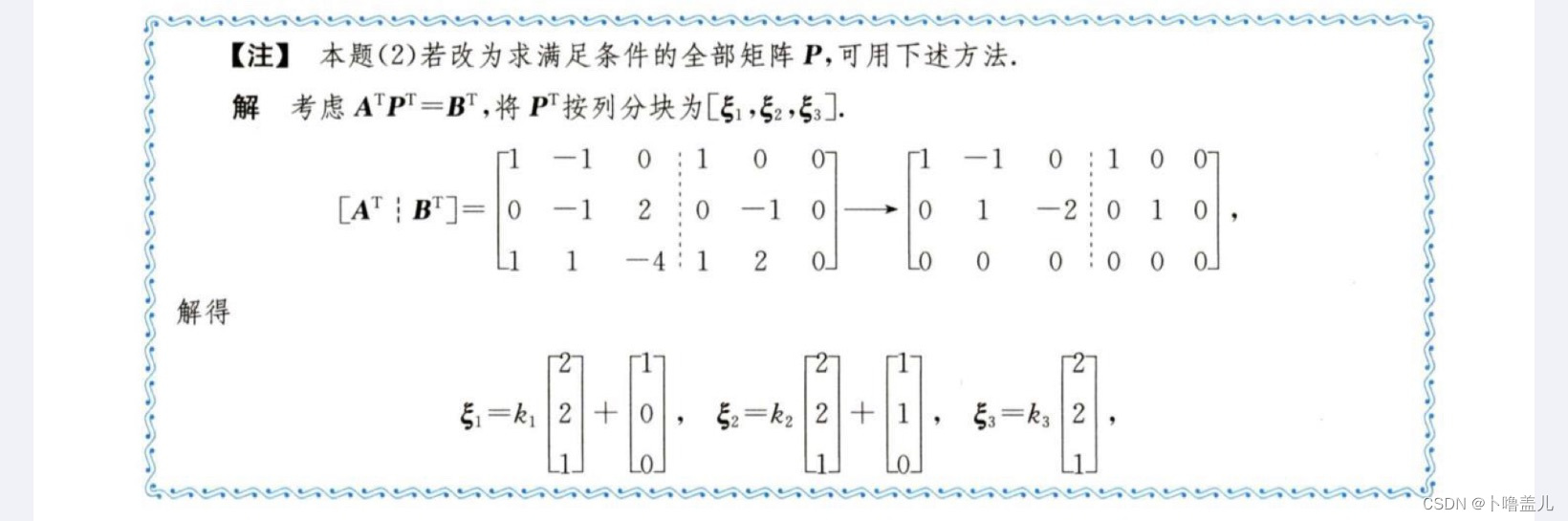

1、幂零矩阵

2、可拆解为A+E型矩阵的运算


3、正交与施密特化
1️⃣正交

2️⃣施密特正交化
意义:将两个线性无关的向量变成正交单位向量。

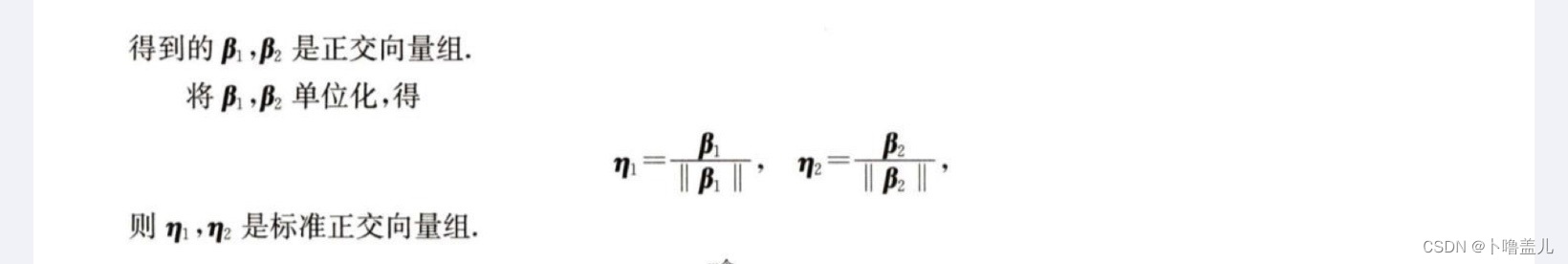
来一道题:


4、 转置+求逆
1️⃣转置运算

2️⃣求逆运算
🔡基本公式A A*=|A|E
🔡A和E拼接、通过初等变换反过来
🔡找到AB=E 的B
🔡将A分解成B·C、A的逆通过简单的BC求
🔡分块矩阵的逆矩阵

5、等价矩阵(已知A和B等价,求全部P)




 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


