便于理解但是不够精确的说法:
熵:一种可能性的所有的信息量
相对熵(KL散度):真实分布与预测的分布的信息量的差(真实-预测),值越小说明与真实约接近。
交叉熵:由kl散度公式变形而得,式子拆开来前半部分是熵后半部分就是交叉熵。因为前面的熵不变,所以优化的时候直接用交叉熵计算损失更加方便。
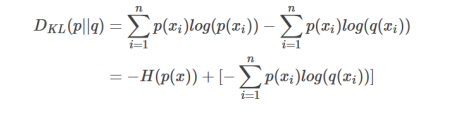 博客记录便于复习与整理,如有不对请指教,谢谢!
博客记录便于复习与整理,如有不对请指教,谢谢!
参考文献
https://blog.youkuaiyun.com/tsyccnh/article/details/79163834
便于理解但是不够精确的说法:
熵:一种可能性的所有的信息量
相对熵(KL散度):真实分布与预测的分布的信息量的差(真实-预测),值越小说明与真实约接近。
交叉熵:由kl散度公式变形而得,式子拆开来前半部分是熵后半部分就是交叉熵。因为前面的熵不变,所以优化的时候直接用交叉熵计算损失更加方便。
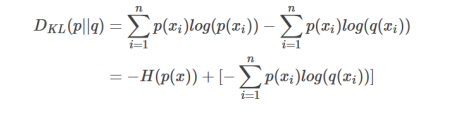 博客记录便于复习与整理,如有不对请指教,谢谢!
博客记录便于复习与整理,如有不对请指教,谢谢!
参考文献
https://blog.youkuaiyun.com/tsyccnh/article/details/79163834
 6144
6144
 4780
4780

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


