熵、相对熵和交叉熵的区别与联系

一.信息量

信息奠基人香农（Shannon）认为“信息是用来消除随机不确定性的东西”，也就是说衡量信息量的大小就是看这个信息消除不确定性的程度。
“太阳从东边升起”，这条信息并没有减少不确定性，因为太阳肯定是从东边升起的，这是一句废话，信息量为0。
”2018年中国队成功进入世界杯“，从直觉上来看，这句话具有很大的信息量。因为中国队进入世界杯的不确定性因素很大，而这句话消除了进入世界杯的不确定性，所以按照定义，这句话的信息量很大。
根据上述可总结如下：信息量的大小与信息发生的概率成反比。概率越大，信息量越小。概率越小，信息量越大。
设某一事件发生的概率为P(x)，其信息量表示为：
$$I(x)=-log(P(x))$$
I(x)表示信息量，log表示以e为底的自然对数。

二.熵（信息熵）

信息熵用来表示所有信息量的期望。
期望是试验中每次可能结果的概率乘以其结果的总和，所以信息量的熵可表示为（这里的X是一个离散型随机变量）：

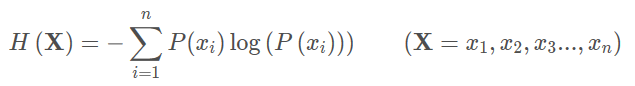
H(X)表示X变量的信息熵，xi表示X不同的取值，例如使用明天的天气概率来计算其信息熵：