第三节课：Manacher算法

---

1.Manacher算法

最长回文字串：左右不分互为逆序。
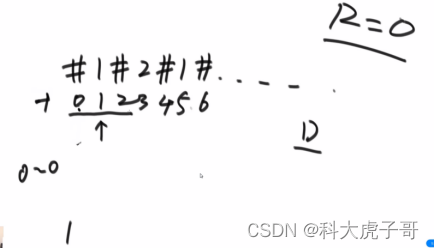
暴力方法：从字符串的每个位置分别向外扩，长度为偶数的回文这种方法没法得到—>在字符串的两端和以及两个字符之间加一个特殊字符（特殊字符可以是字符串中的字符，不影响）。时间复杂度：O(N^2)

Manacher算法是对暴力方法的加速。
回文直径：整个回文的长度；回文半径：从中心（包括）到一端的回文长度–>回文半径数组

之前所有扩的位置中到达的最右回文右边界R：初始值为-1；取得右边界时的中心点c：初始值为-1。两个变量同时更新

(1)当前中心点，这个点没有在回文右边界里–>暴力扩

(2)当前中心点，这个点在回文右边界里

根据i’的回文情况进行分类：
1)i’的回文整个在L…R里–>i的回文半径等于i’

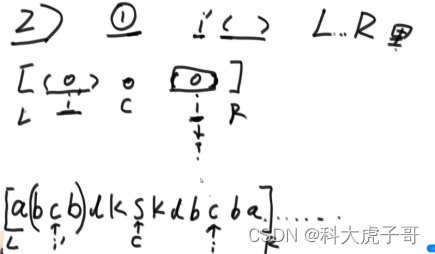
证明不可能更大：

2)i’的回文区域有部分跑到了L的外面–>i的回文半径等于i到R这段

证明：

3)i’的回文区域边界刚好在L–>i的回文半径至少为i到R这段，是否会更长，需要进一步验证

伪代码：

复杂度分析：

代码实现：

string getManacherStr(string& s) {
	int len = s.length();
	string res = "#";
	for (int i = 0; i < len; i++) {
		res += s[i];
		res += "#";
	}
	return res;
}

int manacher(string& str) {//返回最大回文串的长度（直径）
	if (str.length() == 0) {
		return 0;
	}
	string s = getManacherStr(str);//123-->#1#2#3#
	vector<int>pArr(s.length());//回文半径数组
	int C = -1;//中心
	int R = -1;//回文右边界再往右一个位置，最右的有效区是R-1
	int res = INT_MIN;

	for (int i = 0; i < s.length(); i++) {//每个位置都求回文半径
		pArr[i] = i < R ? min(pArr[2 * C - i], R - i) : 1;//各种情况下最少不用扩的区域的半径
		while (i + pArr[i]<s.length() && i - pArr[i]>-1) {//尝试外扩
			if (s[i + pArr[i]] == s[i - pArr[i]]) {
				pArr[i]++;
			}
			else {
				break;
			}
		}
		if (i + pArr[i] > R) {
			R = i + pArr[i];
			C = i;
		}
		res = max(res, pArr[i]);
	}
	return res - 1;
}