堆(利用向下调整来建堆)

堆(heap):
对本质上是一个二叉树,满足这么几个条件:
1.完全二叉树
2.对于数中的任意节点,满足根节点小鱼左右子数的值(小堆);满足根节点大于左右子数的值(大堆);一个堆如果是小堆,就不可能是大堆,堆通常就是通过数组的形式来存储的.
堆最大的用处就是能让我们快速找到一个数中的最大值或者最小值(根节点)
堆的几种常见操作:
一:向下调整
前提:左右子数必须是一个堆才能进行调整;

先设定根节点为当前节点.
找到当前节点的左右子数的值(通过下标来获取到)
比较左右子数的值,找出谁更小,用child标记更小的值.
比较child和parent值谁大谁小
如果child比parent小,不符合小堆的规则,就进行交换.
如果child比parent大,符合小堆的规则,不需要交换,整个调整也就结束了.
处理完一个节点之后,从当前child出发,循环刚才的过程.
借助向下调整,就可以把一个数组构建成堆.
从倒数第一个非叶子节点开始,从后往前遍历数组,针对每个位置,依次向下调整即可.

调整完的堆:

接下来用Java代码来实现一下向下调整这个过程

    // 以小堆为例
    // 通过 size 指定 array 中哪些元素是有效的堆元素
    // index 表示从哪个位置的下标开始调整
    // 左右子树都是堆, 才能进行这样的调整.
    public static void shiftDown(int[] array, int size, int index) {
        int parent = index;
        int child = 2 * parent + 1;  // 根据 parent 下标找到左子树的下标
        while (child < size) {
            // 比较左右子树, 找到较小值
            if (child + 1 < size && array[child + 1] < array[child]) {
                child = child + 1;
            }
            // 经过上面的比较, 已经不知道 child 是左子树还是右子树了.
            // 知道的是 child 下标一定对应左右子树最小值的下标.

            // 拿 child 位置的元素和 parent 位置的元素进行比较
            if (array[child] < array[parent]) {
                // 不符合小堆的规则, 就交换父子节点
                int tmp = array[child];
                array[child] = array[parent];
                array[parent] = tmp;
            } else {
                // 调整完毕, 不需要继续了
                break;
            }
            // 更新 parent 和 child, 处理下一层的数据.
            parent = child;
            child = parent * 2 + 1;
        }
    }

借助向下调整,就可以把一个数组构建成堆.
从倒数第一个非叶子节点开始,从后往前遍历数组,针对每个位置,依次向下调整即可.
例如:给定如下数组:
9 5 2 7 3 6 8
把这个数组建成小堆:
先写成初始堆:

倒数第一个非叶子节点下标为2,针对这个子数进行向下调整,
不需要调整,此时已经满足小堆了,所以继续往下走.
再针对下标为1的节点调整,经过3和5交换,就调整完成.
再针对下标为0的节点调整,9和2交换,9再和6交换.就完成了.

调整完的样子:

代码实现也很简单,循环调用向下调整方法:

  public static void createHeap(int[] array, int size) {
        for (int i = (size - 1 - 1) / 2; i >= 0; i--) {
            shiftDown(array, size, i);
        }
    }

这里的size-1得到的是最后一个叶子节点,再减一除二就得到了最后一个叶子节点的父节点(也就是倒数第一个非叶子节点)

下面来验证一下,将方法合到一起来建堆;

import java.util.Arrays;

// 以小堆为例
public class Heap {
    // 通过 size 指定 array 中哪些元素是有效的堆元素
    // index 表示从哪个位置的下标开始调整
    // 左右子树都是堆, 才能进行这样的调整.
    public static void shiftDown(int[] array, int size, int index) {
        int parent = index;
        int child = 2 * parent + 1;  // 根据 parent 下标找到左子树的下标
        while (child < size) {
            // 比较左右子树, 找到较小值
            if (child + 1 < size && array[child + 1] < array[child]) {
                child = child + 1;
            }
            // 经过上面的比较, 已经不知道 child 是左子树还是右子树了.
            // 知道的是 child 下标一定对应左右子树最小值的下标.

            // 拿 child 位置的元素和 parent 位置的元素进行比较
            if (array[child] < array[parent]) {
                // 不符合小堆的规则, 就交换父子节点
                int tmp = array[child];
                array[child] = array[parent];
                array[parent] = tmp;
            } else {
                // 调整完毕, 不需要继续了
                break;
            }
            // 更新 parent 和 child, 处理下一层的数据.
            parent = child;
            child = parent * 2 + 1;
        }
    }

    public static void createHeap(int[] array, int size) {
        for (int i = (size - 1 - 1) / 2; i >= 0; i--) {
            shiftDown(array, size, i);
        }
    }

    public static void main(String[] args) {
        int[] array = {9, 5, 2, 7, 3, 6, 8};
        createHeap(array, array.length);
        System.out.println(Arrays.toString(array));
    }
}

运行程序得到建堆结果:


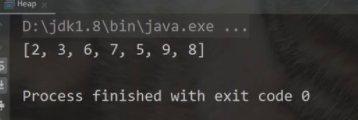
和预期结果一样,建堆完成.