经济时间序列

上图为德国1960至2011年的实际国内生产总值GDP，可以发现这一序列在长期内逐步增长，也就是说有一个正的趋势。另一方面，一年内存在显著的季节性变动。此外，在1990年之后存在结构性变化，这是因为1990年之后德国统一，因此GDP上升较为明显。

上图是GDP数据季度之间的差分序列，可以发现通过差分，时间序列的长期趋势得以消除，但是季节性变化依旧存在。
分析季度到季度的变化率，可以使用季度增长率来表示：

但是这个指标存在一个缺陷，即正向和负向变化的不对称性。比如，从100上升到125，qgr=25%,从125下降至100,qgr=-20%。
为了避免这种情况，人们会使用连续增长率进行替代。
连续增长率：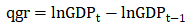

由于ln(1+x)=x,因此当增长率x取值较小时，连续增长率和季度增长率的差异可以忽略。

由于增长率较小的缘故，我们可以发现图二和图三间的差异不是特别大。
上面两张图计算的是季度的增长率，虽然不存在长期趋势，但是存在明显的季节趋势。如果我们想消除季节趋势，那么可以使用年度变化这一指标。
年度变化：


从图中，我们可以看到GDP年度变化多数时间为正，只有在经济衰退时为负值。图形中有几次明显的衰退期：1967年德国遭遇了二战以来的第一次真正衰退；而1975年和1981年、1982年是由石油价格冲击而造成的两次衰退。
同样我们也可以定义年度相对增长率：


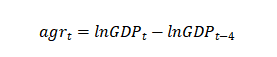
从图中我们可以看到在经历了1975年和80年代初期的两次衰退之后，GDP年增长率基本为正，但和以前相比处在一个较低的水平上。

对于一个时间序列，我们还可以采用一种数据变换手段在消除季节趋势的同时，保留数据的长期趋势，即带平滑的GDP序列。

通过平滑处理，我们可以发现GDP围绕着平滑值呈现上下波动的趋势。而在平滑成分中，我们也清晰地看出了四次经济衰退：即60年代末、70年代中期、80年代初和92年之后。德国统一（90年代中期）这一事件使得序列值显著上升且持续产生影响。此外，我们也可以发现金融危机（2008）也使序列产生了一个向下的位移。
以上案例可以说明，对于一个时间序列数据采取不同的数据变换方法可以获得序列的不同信息。