【数据结构】树 (Trees)

I. 阅读前你所需要的基础知识

1. 了解数组 (array)
2. 此文章内容并非二叉树 (binary tree)，而是普通的树

II. 树 (Trees) 以及其相关术语

• 什么是树：树是一种数据结构，由许多个节点 (node) 和分支 (branch) 构成。下图为一个树，可以发现每一个节点就像现实中的树叶，分支则像树枝，故此结构得名“树”。
  
• 节点：节点是树内存储数据的地方 (例如大图中的A，B，C等等)
• 根节点 (root node): 一个树内最顶端的节点 (例如大图中的A)
• 子树 (subtrees): 子树是一个树内，选择任意一个非根节点作为子树根节点后，形成的树 (例如下图，是大图中的树的一个子树)
  
• 父节点 (parent node): 一个节点的父节点是在上一层级与自己相连的节点 (例如大图中，C是H的父节点，D是J的父节点)
• 子节点 (child node): 一个父节点下一层级中与之连接的任意一个节点 (例如大图中，F是B的一个子节点，I是D的一个子节点)
• 路径 (path): 树内的一个路径是一条由节点组成的序列。在路径中，除了第一个节点以外，其余每一个节点的前一个节点都必须是它的父节点 (例如大图中，{ABG}是一条路径，{AC}是一条路径)
• 路径长度 (path’s length): 一个路径中分支的数量。注意，路径长度并不是一个路径内节点的数量，而是分支数量 (例如路径{ABG}的路径长度为2)
• 节点的度 (degree): 一个节点的度等于其拥有的子节点数量 (例如大图中，A的度为3，D的度为2)、
• 节点的等级 (level) /深度 (depth): 一个节点的等级/深度是指从根节点到当前节点这条路径的长度 (例如H的等级/深度为2)
• 树的高度 (height): 当前树内最长路径的长度，出于计算方便，可以实用这个公式：层级数 - 1 (例如大图中的数的高度为2)
• 节点的高度：以当前节点为子树父节点形成子树，此节点高度即为子树的高度 (例如大图中，B的高度为1，H的高度为0)

III. 树的实现方法

1. 父指针实现 (The parent pointer implementation): 所有的节点被存储在同一容器中，每个子节点会指向其父节点 (此方法泛用性较低，因为我们无法访问一个节点的子节点，只能通过子节点访问父节点)
   

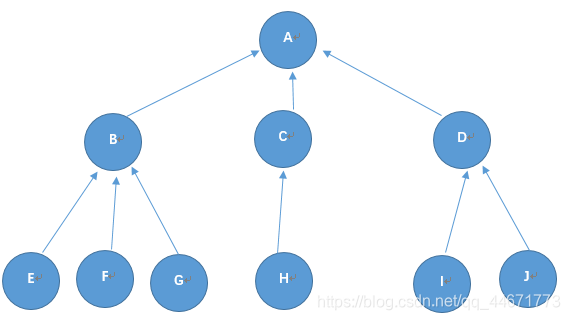
2. 子列表实现 (The list of children implementation): 每个节点有自己独立的一个列表，用于存储其所有子节点 (此方法较为泛用)

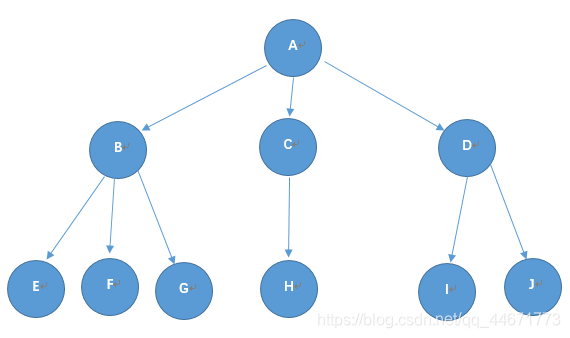
• 子列表实现的“列表”，我应如何选择：
  • 静态数组：如果你每一个节点拥有固定数量的子节点 (例如二叉树)，那么你可以选择用容量不变的静态数组
  • 自动扩容数组：如果你每个节点内的子节点数量不定，但你又比较懒，你可以使用自动扩容数组 (例如C++中的std::vector)。自动扩容数组的缺点在于，他往往会占用多于你需求的内存
  • 链表 (linked list)：如果你每个节点内的子节点数量不定，那链表一定是个不错的选择，它并不会像自动扩容数组一样占用你额外的内存。

感谢您的阅读，如若发现问题请在评论区告知，我会及时修改。