【数据结构】树-概述篇（图解）

GitHub同步更新（已分类）：Data_Structure_And_Algorithm-Review

公众号：URLeisure 的复习仓库
公众号二维码见文末

以下是本篇文章正文内容，下面案例可供参考。

---

什么是树？

• 随着计算机的发展，在数据结构中树被引申为由一个集合以及在该集合上定义的一种关系构成的，由根结点和若干棵子树构成的。

• 前面说的线性表、栈、队列、数组、广义表和字符串，都是一对一的线性关系。

• 现在介绍的树形结构是一对多的非线性关系 。

• 无论是顺序存储，还是链式存储，线性表均有其优缺点。

• 顺序存储可以在 $O(1)$ 时间内找到特定次序的元素，但是插入和删除元素需要移动大量元素，需要 $O(n)$ 时间；

• 而链式存储插入和删除元素需要 $O(1)$ 时间，找到特定次序的元素需要从链表头部向后查找，需要 $O(n)$ 时间。

• 树形结构结合了两者的优点，可以在 $O（logn)$ 的时间内完成查找、更新、插入、删除等操作 。

• 在实际应用中，很多算法都可以借助于树形结构高效地实现。

如何定义树

• 可以从集合论和图论两个角度定义树。
• 我们将从集合论的角度递归定义树，在后续将从图论的角度再次定义树，体会两种定义的不同之处。

树的概念

• 树形结构就像一棵倒立的树，有唯一的树根，树根可以发出多个分支，每个分支也可以继续发出分支，树枝和树枝之间是不相交的。（如果相交，就成图了）
  

• 树（tree）是 n（n ≥ 0）个节点的有限集合，当 n = 0 时，为空树；n > 0 时，为非空树。

任意一棵非空树，满足以下两个条件：

1. 有且仅有一个称为根的节点；

2. 除根结点以外，其余节点可分为 m（m > 0）个互不相交的有限集合 T₁，T₂，…，T_m，其中每一个集合本身又是一棵树，并且称为根的子树。

• 该定义是从集合论的角度给出的树的递归定义，即把树的节点看作一个集合。
• 除了树根以外，其余节点分为 m 个互不相交的集合，每一个集合又是一棵树。

1.树的相关术语

1. 节点：节点包含数据元素及若干指向子树的分支信息。
2. 节点的度：节点拥有的子树个数。
3. 树的度：树中节点的最大度数。
4. 终端节点：度为 0 的节点，又称为叶子。
5. 分支节点：度大于 0 的节点。除了叶子都是分支节点。
6. 内部节点：除了树根和叶子都是内部节点。
   

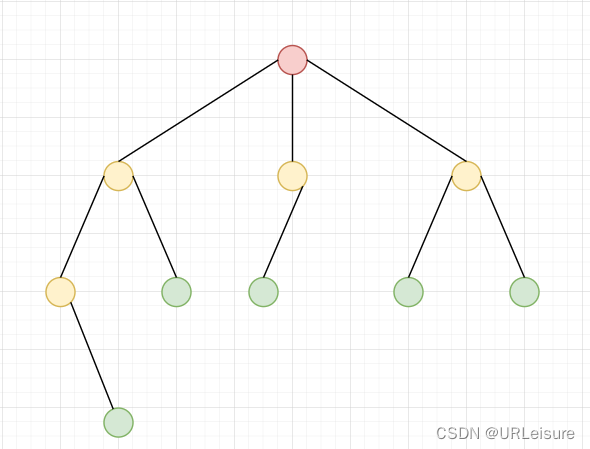
如图，该树的度为 3。

内部节点为黄色，终端节点（叶子）为绿色。

7. 节点的层次：从根到该节点的层数（根节点可以为第 1 层，也可以为第 0 层）。
8. 树的深度（高度）：指所有节点中最大的层数。

9. 路径：树中两个节点之间所经过的节点序列。
10. 路径长度：两节点之间路径上经过的边数。

如图，D 到 A 的路径为 D—B—A，D 到 A 的路径长度为 2。

• 由于树中没有环，因此树中任意两个节点之间的路径都是唯一的。

2.家族树

如果把树看作一个族谱，就成了一棵家族树。

1. 双亲、孩子：节点的子树的根称为该节点的孩子，反之，该节点为其孩子的双亲。
2. 兄弟：双亲相同的节点互称兄弟。
3. 堂兄弟：双亲是兄弟的节点互称堂兄弟。
4. 祖先：从该节点到树根经历的所有节点称为该节点的祖先。
5. 子孙：节点的子树中的所有节点都称为该节点的子孙。
   

D 的祖先为 B、A。

A 的子孙为 B、C、D、E、F、G。

3.其他

1. 有序树：节点的各子树从左至右有序，不能互换位置。
2. 无序树：节点各子树可互换位置。
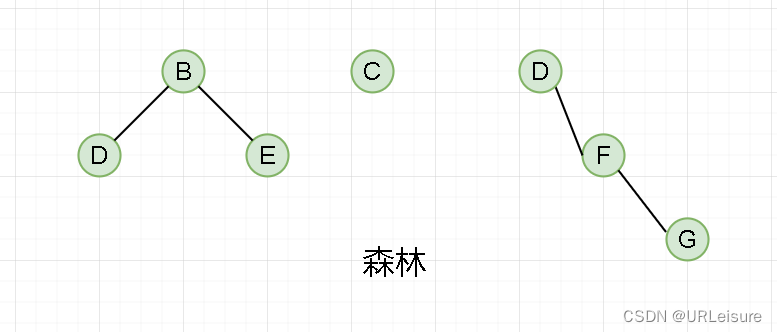
3. 森林：由 m(m ≥ 0) 棵不相交的树组成的集合。

总结

• 明明是一个节点，为什么要交“双亲”？老师说是因为叫“单亲”不好听 = =。

• 原来是 “father”，听说因为平权运动改成 “parent” 了。

---

关注公众号，感受不同的阅读体验

下期预告：树的存储