【Day2】【纪中OJ】2019.1.24大型被虐C组模拟赛（游记+题解）

---

游记

Morning

【Before 8:00】
早餐喝了杯豆浆真开心 （大雾）
【Before 12:00】
C组题目

题目	做法
【东莞市选2008】GCD与LCM	数论
【东莞市选2008】幻灯片	暴力、离散化/扫描线（线段树）
【东莞市选2008】导弹	匈牙利算法、最短路（Floyd）、二分答案/网络流
【东莞市选2008】医院	贪心

**OJ！卡BUG害我有一堆编译错误，害我两题爆0
考试得分：100+0+62.5+0=162.5
实际得分：100+25+62.5+62.5=250
蒟蒻+各位大佬排名

姓名	名次	分数
lyf	1	250
prj	2	225
cnh	3	212.5
…	…	…
我	5	162.5

（查成绩大法好）
我好弱啊
【Before 2:00】
去饭堂取得很早，看到好多大佬腐手机，自己也跟着腐了一把。打开三崩子，刷了一波每日
中午睡得巨香

Afternoon

【Before 5:00】
码了一会儿T1题解，听大佬讲课。
授课名单

题号	评价	授课人
T1	讲得乱七八糟，还被小六大佬砸场子了	蒟蒻本人
T2	大佬强无敌，两个大佬在上面讲一些蜜汁算法（？）	被拉过来的组织授课大佬+lzc小六大佬强
T3	有理有据，令人信服	prj
T4	水分导论	cnh+lyf

难度：第一题<第四题<第三题<第二题

Evening

【Before 10:00】
跑去303听了逆元（一脸懵逼）
后面又讲了一遍T3疯狂玩凤姐梗

---

纪中C组T1-GCD与LCM题解

----------------------一条WA的分界线-------------------------------
【题目描述】给出某两个整数a和b（a<=b）的最大公约数GCD和最小公倍数LCM，请找出满足的a和b，使得b-a的值最小。
【输入】输入数据只有一行，包括两个整数GCD 和LCM。输入保证至少存在一组解。
【输出】输出包含一个整数，为最小的b-a的值。
【样例输入】6 36
【样例输出】6
【数据范围限制】对于50%的数据，1<=a<=b<=10^{3，对于100%的数据，1<=a<=b<=9}10;
-----------------------一条TLE的分界线----------------------------

【难度系数】★★☆☆☆
【核心算法】数论
-----------------------一条MLE的分界线-------------------------------
【思路】由大佬lyf的紧密推算可知样例的两个数分别为12、18，将这两个数用短除法进行运算，草稿如下图：

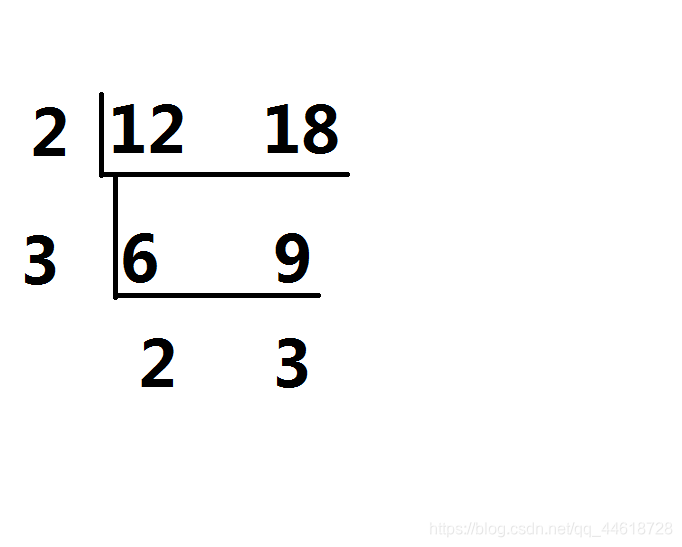
就是：

①我们已知由这些E数列乘起来的最大公因数，以及由E数列和C、D的乘积最小公倍数，所以将最小公倍数除以最大公因数就可以得到C和D的乘积了。又得A=C最大公因数，B=D最大公因数，题意为尽量让B-A最小（就是让B与A尽量接近），所以可得问题为“已知C和D的乘积，使C和D最接近”
②通过大佬prj的推算可知C与D互质，问题升级为“已知C和D的乘积，使C和D最接近并互质”
③关于对“已知C和D的乘积，使C和D最接近”问题的做法，举例：假设CD为6，而在6的因数1、2、3、6中，我们只要知道前一半数1、2，自然就可以得出后一半数3、6。
④求B-A=>D最大公因数-C*最大公因数=>(D-C)*最大公因数
⑤没有了喵~~~~~
-----------------------一条RE的分界线-------------------------------
【代码】

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
ll gcd,lcm,l; 
bool pd(ll x,ll y){
   
   //判断两个数是否互质（对应步骤②） 
	int z;
	while (z=x%y){
   
   
		x=y;
		y=z;
	}
	if (abs(y)==1) return true;
	else return false;
}
int main(){
   
   
	cin>>gcd>>lcm;
	lcm/=gcd;// lcm变为C和D的乘积 
	for (ll i=1;i<=sqrt(lcm);++i)//枚举因数（对应步骤③）
	  if (lcm%i==0&&pd(lcm/i,i)==true) l=lcm/i-i;//C对应i，D对应lcm/i，l记录D-C的差值（对应步骤①） 
	cout<<l*gcd<<endl;//最后将(D-C)*最大公因数gcd并输出（对应步骤④） 
	return 0;
}

大佬传送门
某大佬prj的题解

---

纪中C组T2幻灯片题解

题目描述
给出一张无向的完全图(任意两点之间都有一条边的图)G=(V,E)，它可以表示出某一块大陆的地图：每个顶点表示一座城市，每条边代表连接的两个城市间的距离，该大陆任两个城市都是直接连通的。另外在这个大陆上有两个特殊的国家，我们称为A国与B国，其中A国有N个城市，B国有M个城市。这里A国相对于B国来说是一个大国（我们有N>=M），而且它最近发明了一种新型武器：响尾蛇导弹（A Crotalid Missile），这种武器威力十分巨大，以至于每枚导弹都可以摧毁任意一座城市。A国总统在战略安排上要求A国管辖的每个城市都配备一枚这种响尾蛇导弹。B国窃取到了这个情报，B国总统当然不能坐以待毙，他感觉受到了强大的威胁，于是要求他们的科学家们尽快研制出一个导弹防御系统来抵御将来可能遭受的攻击。当然这个防御系统必须是可靠且有效的，因此在制造系统之前B国的科学家们必须首先考虑清楚该系统的反应速度如何确定。所以作为B国最聪明科学家之一的你，必须尽快算出A国要摧毁B国所有城市至少需要的时间是多少。

输入
输入第一行为一个整数K（2<=K<=100），表示这块大陆的顶点数。接下来K行，每行包含K个整数，描述了城市的连接情况。这个K*K的矩阵中，matrix[i][j]表示城市i到城市j的距离，这也是导弹由城市i到城市j间的飞行时间。这里有：matrix[i][j]=matrix[j][i]，matrix[i][i]=0，1<=matrix[i][j]<=100。接下来一行为整数N，1<=N<=K，为A国的城市数。下面一行N个整数，列出A国管辖的城市编号. 再下来一行为整数M，1<=M<=N，为B国的城市数。下面一行M个整数，列出B国管辖的城市编号。A国与B国管辖的所有城市编号均不相同。

输出
输出文件只有一行，为导弹摧毁B国所有城市至少所需要的时间。

样例输入
3
0 2 1
2 0 10
1 10 0
1
2
1
3

样例输出
3
-----------------------一条WA的分界线-------------------------------
【难度系数】★★★★★
【核心算法】暴力、离散化
【思路】
①这道题正常来说是二维数组模拟计数器，但由于X1,Y1,X2,Y2<=10^9的不正常数据，只能用离散化做。
②对于离散化，先要给x轴y轴排序去重，然后要找出边界坐标对应离散后的坐标数组的下标。
③在离散后的棋盘坐标上标记染色并统计
④有些大佬说要加减0.5，感觉不需要这么精密啊
⑤没有了喵
-----------------------一条RE的分界线-------------------------------
代码

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
const int maxn=105;   //最大矩阵数
const int maxcolor=100005;  //最大颜色编号
struct Rec{
   
                  //矩阵的存储结构
    int x1,y1,x2,y2,c;
}r[maxn];
int x[maxn*2],xn;     //x坐标数值的数组，不同的x坐标总数
int y[maxn*2],yn;     //y坐标数值的数组，不同的y坐标总数
int col[maxn*2][maxn*2];  //各个离散棋盘块的颜色
char mark[ma