N - Trailing Zeroes (III)（阶乘后导0+数论结论+二分）

Forward in time

于 2019-08-13 16:59:31 发布

阅读量162

点赞数

CC 4.0 BY-SA版权

分类专栏：数论二分

本文链接：https://blog.youkuaiyun.com/qq_44555205/article/details/99449234

数论同时被 2 个专栏收录

40 篇文章

订阅专栏

二分

5 篇文章

订阅专栏

本文介绍了一种使用二分查找算法求解给定阶乘尾部零数对应最小n值的方法。通过分析n!尾部零数与5的因子数量的关系，利用二分查找快速定位满足条件的最小n值。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

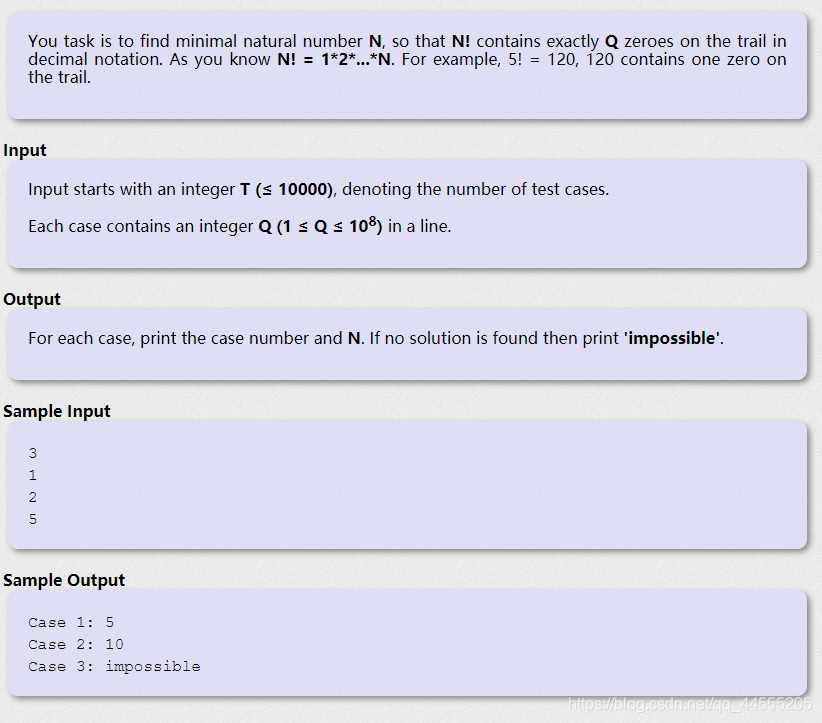
在这里插入图片描述
题目意思很简单，给你Q表n阶乘的后导0个数，然后求n的最小值；
这里有个数论结论，就是n!尾部数的个数就是n!的5的因子的个数；
所以可以用一个while循环算出n!的尾部0个数；因为这里是要求最小的n，比如：10！和14阶乘它们尾部的0的个数都是一样的所以10是最优选择，所以需要最后处理一下；
然后就是怎么找这个n了，我可以用二分来找这个n使得n!这个后导0个数等于Q
所以AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll INF=0x3f3f3f3f;
ll Num(ll n){//求n!的后导0个数
	  ll res=0;
	  while(n){
	  	  res+=n/5;
	  	  n/=5;
	  }
	  return res;
}
int main(){
	ll T,Q,g=1;
	scanf("%lld",&T);
	while(T--){
		scanf("%lld",&Q);
	 ll down=0,up=INF,mid;
	 while(down<=up){//二分
	 	mid=(down+up)/2;
	 	  if(Num(mid)>Q){
	 	  	up=mid-1;
		   }else if(Num(mid)<Q){
		   	down=mid+1;
		   }else break;
	 }
	 if(Num(mid)==Q)printf("Case %lld: %lld\n",g++,mid-mid%5);//注意好这里需要特殊处理一下；可以从5的倍数上去理解
	  else printf("Case %lld: impossible\n",g++);
	}
}