李宏毅 SVM (support vector machine)

SVM组成

Hinge Loss讲解
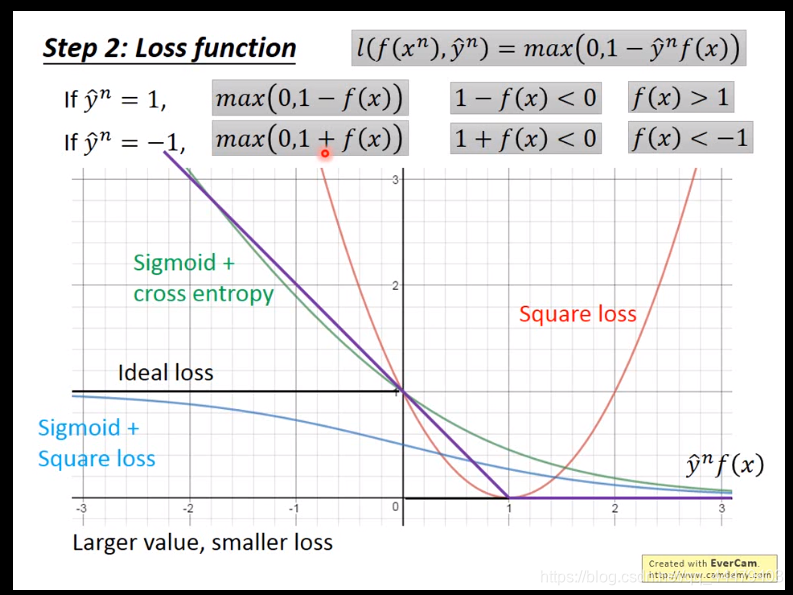
loss function不可微分，所以换成另一个函数。可以微分。输入x输出正负1。

g（x）里边有f（x）函数。并且y^乘以f（x）是横轴。纵轴为loss值。理想下越往右loss越小。square loss就是做差求平方，但是用到binary classfity上是不合理的。

理想的loss函数。sigmoid + square loss函数下边的计算公式。

sigmoid+square loss横轴非常小的时候，实际上可以很大程度上gradient，但是调整横轴变大的时候，loss变化的却不大，所以努力了没有回报，sigmoid+ cross entropy相反，调整横轴loss变化的大符合实际，努力有回报，train的更快更容易，所以他很愿意把糟糕的值往正了推，所以大多情况下用cross entropy。
解决分类问题交叉熵公式：


hinge loss如下图；在0和后边函数之间取最大值。在训练时f（x）太大或者太小，对于hinge loss无影响，hinge loss只要做到f（x）大于1或者小于-1就行。hinge loss是紫色的线段。如图可知紫色线横坐标可知大于1就好再大也没有什么帮助。

逻辑回归和线性svm不同之处就是loss function ；逻辑回归loss function是cross entropy 解决分类问题；线性svm就是hinge loss分类问题 如下图所示，它是一个凸函数无论从哪里进行梯度下降都能找到loss最小。

linear svm可以用gradient descent来更新参数w如下图；

这个loss函数的形式就是我们常见的svm loss 函数。把之前的loss 函数分解成俩个公式，但是意思是一样的。

svm分类的时候只考虑支持向量机就是an不等于零的data points，logistic regression所有的data points全考虑进行分类。an就是之前f（x）对hinge loss求导的值（gradient d）一个是零另一个不等于零。

w写成an与xn的sum之和，xn是data points 也是train set；之后进行一系列运算得到model f（x）等于an与kernel函数的sum。an不等于零的参与运算。kernel 函数就是输入x与所有xn进行内积（Inner product）；

唯一不知道的事an，找到an是loss function最小；loss function 换算如下图，只需要知道kernel的值即x与z的内积。不需要知道输入向量x的样子，这种方法叫kernel trick（内核技巧）。svm也可以用。

k（x，z）比进行先做特征转换+内积快得多。计算如下；

多维的x进行kernel操作计算；
Radial Basis Function Kernel（径向基核函数）
在无穷多维空间中做内积，可能产生过拟合，在train是准确度高，test是不好。计算如下图；

sigmoid kernel
kernel计算K（x,z）就是输入vector x与train set里的每一个vector z进行内积计算；
泰勒展开公式：
输入vector x 对每一个train set vector x 进行内积，如下图计算。下图tanh的操作与神经网络联系起来讲解；trian set的vector z 是支持向量机，an不等于零的data point。
直接设计kernel k（x，z），不用理会x，z的feature长什么样。把x，z带进kernel就会得到一个在高维空间的内积的vector，所以不用理会x，z长什么样。svm进行语音分类举例子;一段声音讯号，无法用一个vector来描述它，长度不同，无法描述。直接定义kernel k（x，z），一段声音讯号x带进去另一段声音讯号z带进去能够得到什么结果定义好，就不用知道x，z的声音信号描述成vector是什么样的。

获取以上文本PPT请点击这里