树形结构+dp思维 Codeforces Round #247 (Div. 2) C题 k-Tree

k-Tree

Quite recently a creative student Lesha had a lecture on trees. After the lecture Lesha was inspired and came up with the tree of his own which he called a k-tree.

A k-tree is an infinite rooted tree where:

· each vertex has exactly k children;
· each edge has some weight;
· if we look at the edges that goes from some vertex to its children (exactly k edges), then their weights will equal 1, 2, 3, …, k.

The picture below shows a part of a 3-tree.

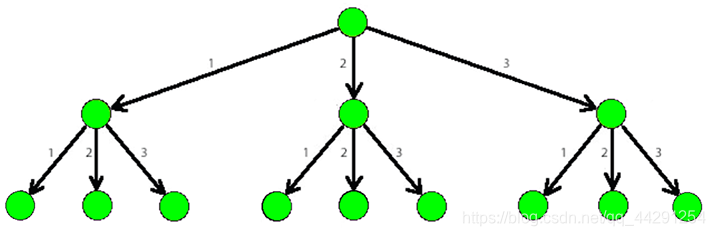
As soon as Dima, a good friend of Lesha, found out about the tree, he immediately wondered: “How many paths of total weight n (the sum of all weights of the edges in the path) are there, starting from the root of a k-tree and also containing at least one edge of weight at least d?”.

Help Dima find an answer to his question. As the number of ways can be rather large, print it modulo 1000000007 (109 + 7).

---

题目大意：说明了 k 树的定义，然后问你从 1（根结点）开始，往下走，权值和为 n 的路径条数，要求路径上至少有一条边权值大于等于d；

虽然是涉及到了树的结构，但是和树没有太大关系，可以设：

dp1[i]+=dp1[j] (j>=i-k&&j<i) 表示组成 i 的路径条数；

dp2[i]+=dp2[j] (j>=i-d+1&&j<i) 表示组成 i 的路径条数，但是这个 i 本身就小于 d；

所以，dp1[n]-dp2[n] 就是答案要求的路径条数；

代码：

#include<bits/stdc++.h>	
#define