朴素贝叶斯（NB）

生成模型：是一种条件概率。常见的有隐马尔科夫模型，朴素贝叶斯，
判别模型：SVM，逻辑回归，条件概率
伯努利分布：只有0-1两种情况，例如抛硬币事件。伯努利试验是只有两种可能结果的单次随机试验
二项分布：n重伯努利试验成功次数的离散概率分布，伯努利分布是二项分布在n=1时的特例。二项分布名称的由来，是由于其概率质量函数中使用了二项系数
多项分布：二项式分布的推广。如果现在还是做n次试验，只不过每次试验的结果可以有多m个，且m个结果发生的概率互斥且和为1，则发生其中一个结果X次的概率就是多项式分布。扔骰子是典型的多项式分布
共轭分布：先验概率与后验概率有相同的格式
狄利克雷分布(Dirichlet distribution)是多项分布的共轭分布，也就是它与多项分布具有相同形式的分布函数。
先验概率：事情未发生之前，对该事估计、分为客观先验概率（利用过去历史资料），主观先验概率（什么都没有，主管猜测），
后验概率：似然函数以及共轭分布
高斯分布：又叫做正太分布。正态曲线呈钟型，两头低，中间高。

若随机变量X服从一个数学期望为μ、方差为σ^{2的正态分布，记为N(μ，σ}2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
1.朴素贝叶斯模型：有监督的算法，生成模型，简单易于实现，线性模型

朴素：条件独立，也就是说在类别确定的条件下，各个特征是条件独立的
朴素贝叶斯的形式：高斯贝叶斯，和专门用与文本分类的多项式贝叶斯
高斯贝叶斯：专门解决特征值是连续的参数估计

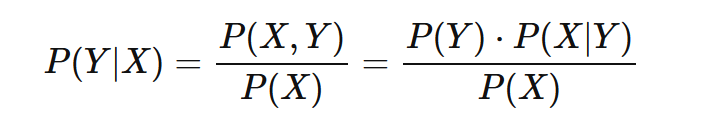
上式中Ck为Y的第k类类别。μk和σ2k

为需要从训练集估计的值。

GaussianNB会根据训练集求出μk和σ2k
。 μk为在样本类别Ck中，所有Xj的平均值。σ2k为在样本类别Ck中，所有Xj

的方差。

GaussianNB类的主要参数仅有一个，即先验概率priors
多项式贝叶斯：假设每个类别下的所有特征服从一个不考虑次序多项式分布

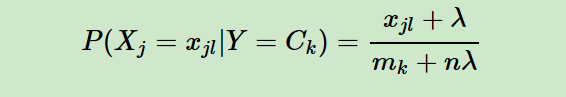
其中，P(Xj=xjl|Y=Ck)是第k个类别的第j维特征的第l个个取值条件概率。mk是训练集中输出为第k类的样本个数。λ 为一个大于0的常数，常常取为1，即拉普拉斯平滑。也可以取其他值
三个参数，alpha及入，默认1，可以调优的时候大一点或者小点
布尔参数fit_prior表示是否要考虑先验概率，如果是false,则所有的样本类别输出都有相同的类别先验概率。否则可以自己用第三个参数class_prior输入先验概率，或者不输入第三个参数class_prior让MultinomialNB自己从训练集样本来计算先验概率，此时的先验概率为P(Y=Ck)=mk/m。其中m为训练集样本总数量，mk为输出为第k类别的训练集样本数。总结如下：

fit_prior class_prior 最终先验概率
false 填或者不填没有意义 P(Y=Ck)=1/k
true 不填 P(Y=Ck)=mk/m
true 填 P(Y=Ck)=class_prior
伯努利贝叶斯模型：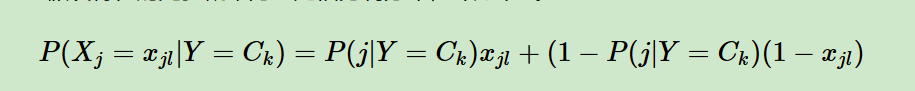
此时l只有两种取值。xjl只能取值0或者1。
BernoulliNB一共有4个参数，其中3个参数的名字和意义和MultinomialNB完全相同。唯一增加的一个参数是binarize。这个参数主要是用来帮BernoulliNB处理二项分布的，可以是数值或者不输入。如果不输入，则BernoulliNB认为每个数据特征都已经是二元的。否则的话，小于binarize的会归为一类，大于binarize的会归为另外一类。

朴素贝叶斯优点：稳定，适用于小规模数据，能处理多分类任务，对缺失数据不太敏感，常用文本分类
缺点：它假设是各个属性间条件独立，但事实上很多属性都有关系，必要知到先验概率，对输入数据的表达形式很敏感
常用的库：GaussianNB 高斯贝叶斯，样本特征的分布大部分是连续值，MultinomialNB 多项式贝叶斯，样本特征的分大部分是多元离散和BernoulliNB 伯努利贝叶斯，样本特征是二元离散值或者很稀疏的多元离散值
朴素贝叶斯面试总结请参考：https://blog.youkuaiyun.com/jingyi130705008/article/details/79464740
日推音乐一首《一只蠢萌家的盥洗室》