图论——二分图——二分图染色（1.0版）

一、定义

二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

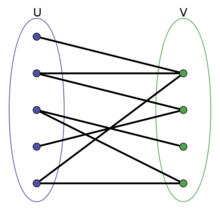
这里是引用

二、二分图的判定

理论上： 无向图G为二分图的充分必要条件是，G至少有两个顶点，且其所有回路的长度均为偶数。

所以注意！！：存在奇数环的一定不是二分图。

实际代码判定：可以通过bfs， dfs 二分图染色判定， 注意多个连通分支的情况

思想是：
对于当前顶点 与其相连肯定 不在同一个集合 所以染成 异色， 前提该顶点没染色。
如果相连的且已经染过色， 就判断颜色是否相同， 相同就不是二分图。

下面是从顶部通过bfs染色的样例图：

—————————————————————————————————————————
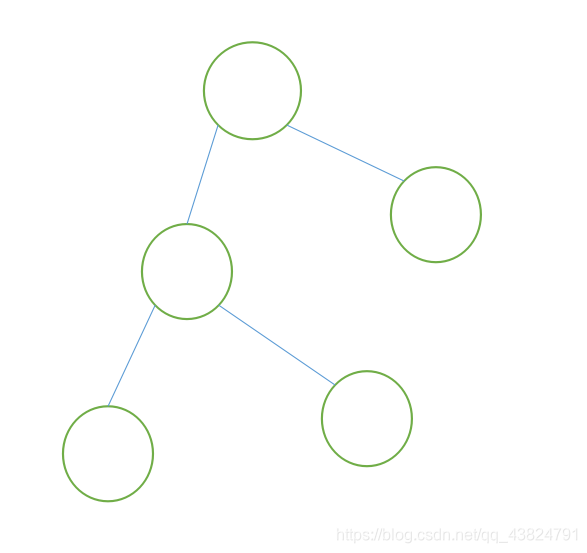
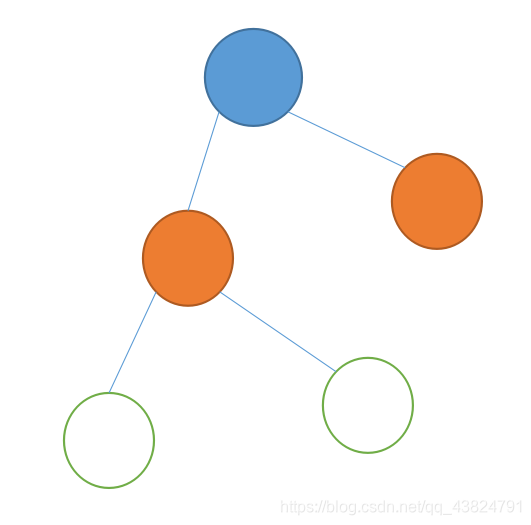
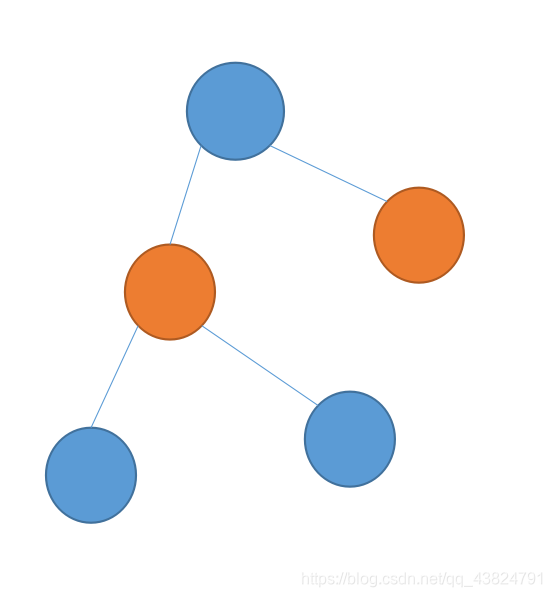
给予这种思想要灵活的运用， 比如hdu4751， 这个题有点转弯。

代码实现：

①bfs

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e3;
int G[maxn][maxn];//邻接矩阵存图

int vis[maxn]; /***染色 标记数组 0表示未染色 -1 1 表示不同的颜色***/

bool bfs(int s, int c)
{
    queue<int>q;
    q.push(s);
    vis[s] = c;
    
    int x;
    while(!q.empty())
    {
        x = q.front();
        q.pop();
        for(int y = 1;y <= N;y++)
        {
            if(G[x][y])
            {
                if(vis[y] ==0) vis[y] = vis[x] == -1?1:-1;/***对相连 且未染色的染成 异色**/
                else if(vis[y] == vis[x])return false; /****如果相连 且染色 判断 是否颜色相同**/
            }
        }
    }
    
    return  true;
}

int main()
{
    /*********
    假设 图已经构造好
    *********/
    int f = 1;//标志，  1  为染色 成功， 0 为失败
    
    memset(vis, 0, sizeof(vis));    
    
    for(int i = 1;i <= N;i++)//N表示顶点， 可能有多个连通分支， 所以要每个点都循环一遍
    {
        if(vis[i] == 0)/******/
        {
            if(!bfs(i, 1))
            {
                f = 0;
                break;
            }
        }
    }
    return 0;
}

②dfs：
dfs 就是 把 bfs 改成dfs 实现， 下面是代码

#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
 
const int MAX_N =105;
int V,E;
// 使用邻接表模拟一张无向图
vector<int> G[MAX_N];
// 顶点的颜色,初始化为0，上色有两种颜色（0 or 1）
int color[MAX_N];
 
bool dfs(int v, int c)
{
    color[v] = c;       // 把顶点染成c
    for(int i = 0; i < G[v].size(); i++)
    {
        // 如果当前点的相邻的点同色就返回false
        if(color[G[v][i]] == c)
            return false;
        // 如果当前点的邻点还没被染色，就染成-c
        if(color[G[v][i]] == 0 && !dfs(G[v][i], -c))
            return false;
    }
    // 如果当前点都被染过色，就返回true
    return true;
}