整除光棍

最新推荐文章于 2020-02-01 12:30:05 发布

原创最新推荐文章于 2020-02-01 12:30:05 发布 · 457 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#整除光棍，大叔模拟

[ 比赛题 ] 专栏收录该内容

17 篇文章

订阅专栏

这篇博客探讨了如何找到一个不以5结尾的奇数对应的光棍数（只包含1的数）及其位数，并解决因数值过大而带来的存储问题。通过模拟除法过程，将大数分解为数组，逐位进行运算，直至找到能被光棍数整除的另一个数。举例展示了具体步骤，帮助理解这一算法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在这里插入图片描述
一、题意：就是给你一个不以5结尾的奇数找到对应的光棍数的位数，和其被光棍数整除的另一个数。
二、难点：该数光棍数和另一个数特别大，难以储存。
三、解决办法呢：
对于另一个数：可以把他每一位储存在数组里；
对于光棍数的查找：可以通过模拟除法过程：至于这个过程是什么，请看下面↓；
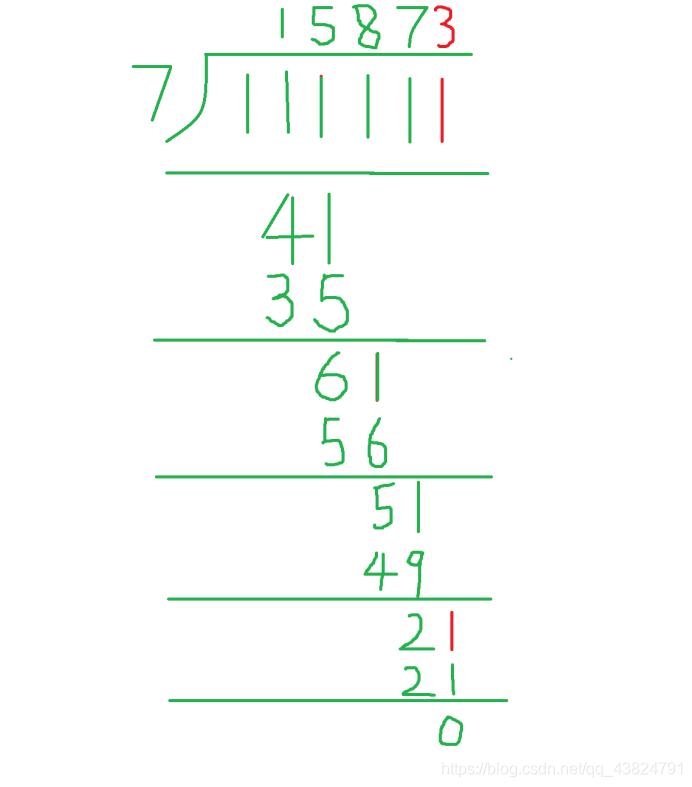
四、寻找光棍数的过程：
1、首先找到第一个不小于该数的光棍数，
2、对其取余，如果余数不为零，下一步操作
3、在该光棍数后面再加1，接着余数进行操作，
4、重复2，3；

如果还不明白，就看一下图片（我一贯讲究NPNBB，翻译：没有图片别BB，所以图片来之不易，凑合看吧，看不懂可以尽情的喷）

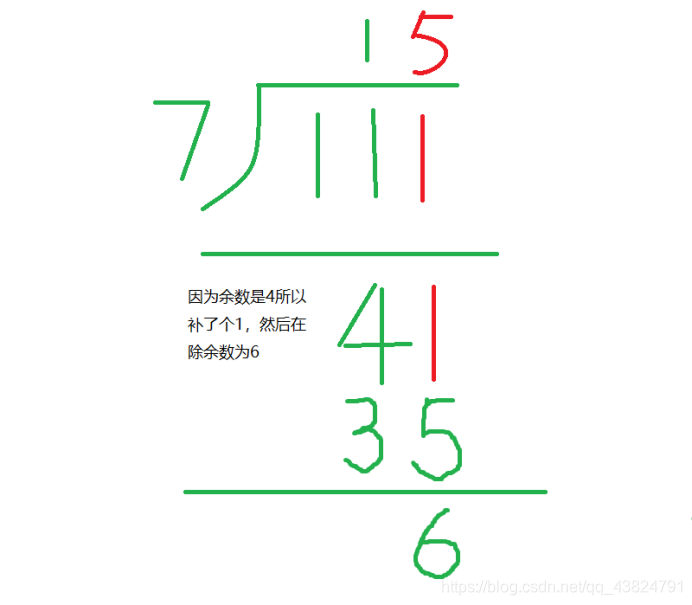
在这里插入图片描述
————————————————————————————————————

————————————————————————————————————————————
因为上一步余数为6， 6!= 0 所以继续在后面补1，然后在除，余数为5
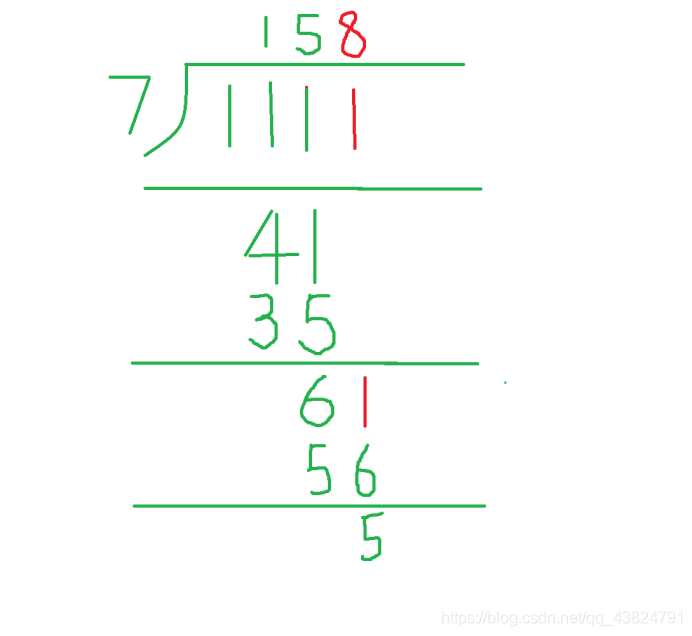
在这里插入图片描述
————————————————————————————————————————
上一步余数为5 ， 5!= 0 ，继续补1，。。。。。。

—————————————————————————————————————————————————
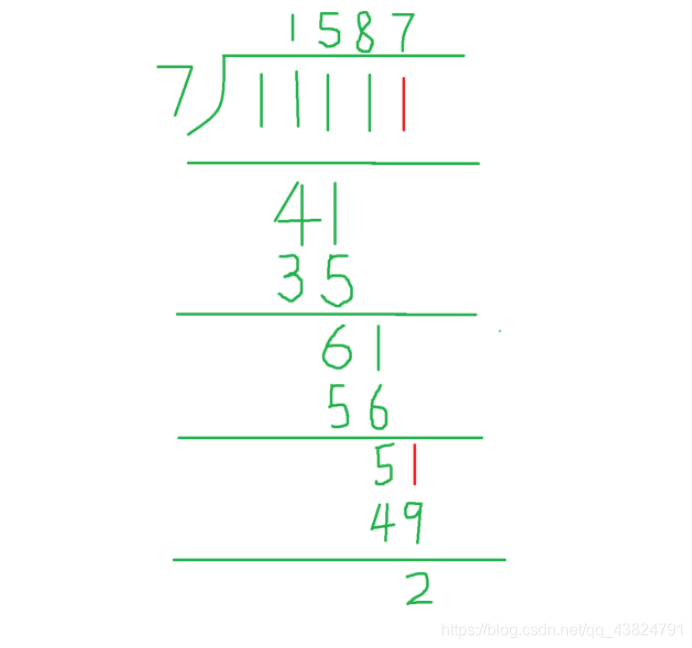
上一步余数为2 ，继续补1，然后再除，余数为 0 ，结束 15873 就是另一个数，光棍数有6个1.

在这里插入图片描述

#include <stdio.h>
#include <stdlib.h>

int main()
{
    int x, l = 1;//x表示输入的奇数， l表示光棍树
    int n = 1;//统计位数；

    int num2[3005];//储存n， 另一个数
    int i = 1;//表示第几位

    scanf("%d", &x);

    while(l< x)//找到不小于该数的第一个光棍数
    {
        l = l*10+1;
        n++;
    }

    int mod;

    while(1)
    {
        mod = l%x;
        if(mod == 0)
        {
            num2[i] = l/x;
            break;
        }
        else //位数不够，加一位
        {
            num2[i++] = l/x;
            n++;
            l = mod*10+1;
        }
    }

    int j;
    for(j = 1;j<=i;j++)
    {
        printf("%d", num2[j]);
    }

    printf(" %d", n);

    return 0;
}