本文通过数学建模方法，分析高温作业专用服装的设计，考虑不同环境温度下，如何选择II层和IV层的最优厚度，以保证假人皮肤外侧温度不超过规定值并限制超温时间。采用假设简化问题，利用Fourier热传导定律建立模型，并通过有限差分格式求解。通过二分法和遗传算法找到最佳厚度，最终给出MATLAB代码实现。
- 题目
在高温环境下工作时，人们需要穿着专用服装以避免灼伤。专用服装通常由三层织物材料构成，记为I、II、III层，其中I层与外界环境接触，III层与皮肤之间还存在空隙，将此空隙记为IV层。
为设计专用服装，将体内温度控制在37ºC的假人放置在实验室的高温环境中，测量假人皮肤外侧的温度。为了降低研发成本、缩短研发周期，请你们利用数学模型来确定假人皮肤外侧的温度变化情况，并解决以下问题：
(1) 专用服装材料的某些参数值由附件1给出，对环境温度为75ºC、II层厚度为6 mm、IV层厚度为5 mm、工作时间为90分钟的情形开展实验，测量得到假人皮肤外侧的温度（见附件2）。建立数学模型，计算温度分布，并生成温度分布的Excel文件（文件名为problem1.xlsx）。
(2) 当环境温度为65ºC、IV层的厚度为5.5 mm时，确定II层的最优厚度，确保工作60分钟时，假人皮肤外侧温度不超过47ºC，且超过44ºC的时间不超过5分钟。
(3) 当环境温度为80时，确定II层和IV层的最优厚度，确保工作30分钟时，假人皮肤外侧温度不超过47ºC，且超过44ºC的时间不超过5分钟。
附件1. 专用服装材料的参数值
附件2. 假人皮肤外侧的测量温度
题目下载地址：http://special.univs.cn/service/jianmo/sxjmtmhb/2018/0709/1179372.shtml
-
解答如下：
-
假设：
假设 1： 假设在整个过程中外部温度保持不变；
假设 2： 假设在整个的过程中只考虑热传导这一种热传递方式， 热对流以及热辐射可以
忽略；
假设 3： 假设织物材料无褶皱且其表面温度处处相同；
假设 4： 假设在实验中热传导的方向与假人人体垂直；
假设 5： 假设假人可以承受实验中所达到的所有可能温度；
假设 6： 假设每一层的参数固定不变， 即不会随着温度的改化发生变化；
假设 7： 假设专用服装的初始温度与假人体内温度一样， 为 37℃；
问题(1)
为了求出温度的分布， 我们需要通过建立温度——外部到假人皮肤之间的距离——时间的数学模型（示意图如下图）
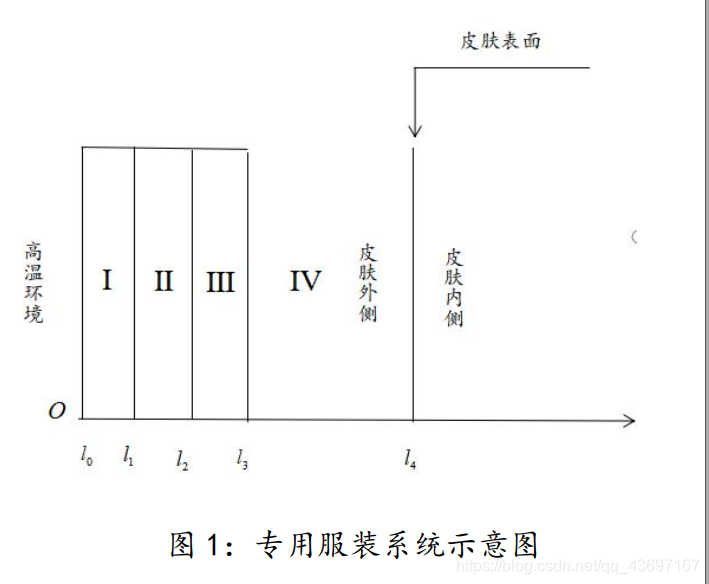
用微元法来建立热防护服系统的热量传递模型
微元［ｘ，ｘ＋Δｘ］在时间段［ｔ，ｔ＋Δｔ］内吸收的热量为：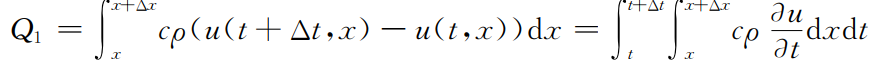
Ｆｏｕｒｉｅｒ热传导定律
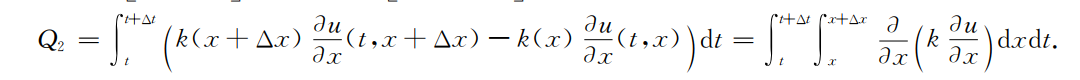
Q1=Q2
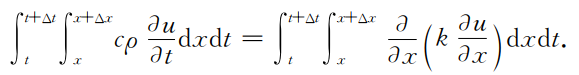
上述方程在各层之间的区间内成立
边界条件：
左边界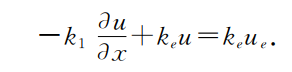
右边界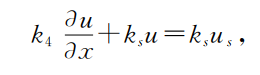
交界面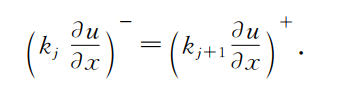
热防护服系统热量传递的偏微分方程模型：
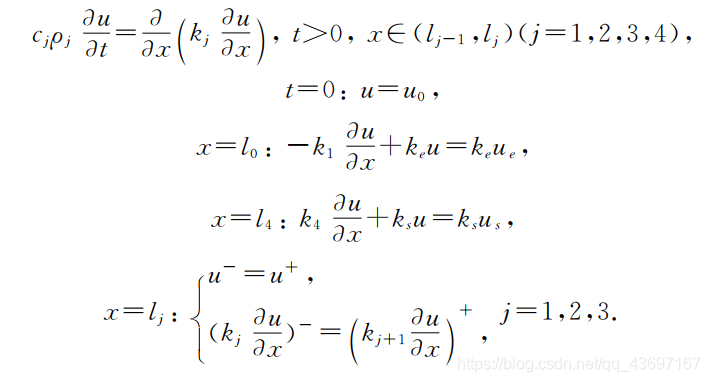
再通过有限差分格式求解：
ks为第四层与皮肤之间的热交换系数 ks=8.36
ke为第Ｉ层与高温环境之间的热交换系数 ke=117.40
(2)这里用的二分法，在满足条件的情况下，求最小的厚度
L2=17.6609mm
(3)这问要求第二层，第四层的最优厚度，双目标最优函数，看了一下各路大神的思路，无非就是遗传算法，暴力穷举，个人认为这里将主要考虑的是产品的成本，皮肤外侧温度随着第二层、第四层厚度的增加而降低的，这个是可以验证的，第四层越厚，第二层必然就会薄一些， 成本自然就低一些，而第四层厚度的增加，所需要的服装材料几乎没有变化。所以我这里将第四层的厚度取最大，将第四层厚度确定之后，这个问题就转化成第二问的问题了，这样就很简单了。
L2=19.2813mm
L4=6.4mm -
具体代码如下：
问题（1）
%问题一的主函数 T1.m
clc
clear;
T=1; %时间步长
m=[6 60 36 50];%将每一层细分为0.1mm每块
%m=[30 300 180 250] %将每一层细分为0.02mm每块
ms=[0 0 0 0]; % ms表示总的分层数
ms(1,1)=m(1,1);
for j=2:4
ms(1,j)=ms(1,j-1)+m(1,j);
end
l=[0.6 6.6 10.2 15.2]*10^(-3); %l1 l2 l3 l4z的坐标
p=[300 862 74.2 1.18]; %各层密度
c=[1377 2100 1726 1005]; %比热
k=[0.082 0.37 0.045 0.028]; %热传导率
u0=37.0; %初始温度
ue=75;
%求空间步长
x=zeros(1,4);
x(1,1)=l(1,1)/m(1,1);
for j=2:4
x(1,j)=(l(1,j)-l(1,j-1))/m(1,j);
end
% M(1,j) 从第1层到第j层的等分数
M(1,1)=m(1,1);
for j=2:4
M(1,j)=M(1,j-1)+m(1,j);
end
%求式（10）里的λ，用b表示λ
for j=1:4
b(1,j)=(k(1,j)*T)/(c(1,j)*p(1,j)*(x(1,j)^2));
end
ke=117.4035;
e=(ke*x(1,1)/k(1,1)); %求式（12）的ue 用e表示
ks=8.36;
us=(ks*x(1,4)/k(1,4)); %求式（13）的us
for j=1:4
v(1,j)=k(1,j)/x(1,j); %求式（14）的v
end
u=zeros(5400/T+1,ms(1,4)+1); %建立一个以距离为x轴，时间为y轴的坐标轴
u(1,:)=37; %时间t=0时，各点温度为37度
f=zeros(ms(1,4)+1,1); %AX=f
x01=e+1; %l0的边界条件
x02=-1;
x1=[-b(1,1) 1+2*b(1,1) -b(1,1)]; %第一层
x2=[-b(1,2) 1+2*b(1,2) -b(1,2)]; %第二层
x3=[-b(1,3) 1+2*b(1,3) -b(1,3)]; %第三层
x4=[-b(1,4) 1+2*b(1,4) -b(1,4)]; %第四层
x12=[-v(1,1) v(1,1)+v(1,2) -v(1,2)]; %12层边界
x23=[-v(1,2) v(1,2)+v(1,3) -v(1,3)];%23层边界
x34=[-v(1,3) v(1,3)+v(1,4) -v(1,4)];%34层边界
x51=-1; %l4的边界条件
x52=1+us;
A=zeros(ms(1,4)+1,ms(1,4)+1);
A(1,1)=x01;
A(1,2)=x02;
f(1,1)=e*ue;
for i=2:ms(1,1)
A(i,i-1:i+1)=x1;
f(i,1)=37;
end
A(ms(1,1)+1,ms(1,1):ms(1,1)+2)=x12;
f(ms(1,1)+1,1)=0;
for i=ms(1,1)+2:ms(1,2)
A(i,i-1:i+1)=x2;
f(i,1)=37;
end
A(ms(1,2)+1,ms(1,2):ms(1,2)+2)=x23;
f(ms(1,2)+1,1)=0;
for i=ms(1,2)+2:ms(1,3)
A(i,i-1:i+1)=x3;
f(i,1)=37;
end
A(ms(1,3)+1,ms(1,3):ms(1,3)+2)=x34;
f(ms(1,3)+1,1)=0;
for i=ms(1,3)+2:ms(1,4)
A(i,i-1:i+1)=x4;
f(i,1)=37;
end
A(ms(1,4)+1,ms(1,4))=x51;
A(ms(1,4)+1,ms(1,4)+1)=x52;
f(ms(1,4)+1,1)=us*u0;
%追赶法
a=zeros(1,ms(1,4)+1);%下对角元素
a(1,1)=0;
for i=2:ms(1,4)+1
a(1,i)=A(i,i-1);
end
c=zeros(1,ms(1,4)+1);%上对角元素
c(1,ms(1,4)+1)=0;
for i=1:ms(1,4)
c(1,i)=A(i,i+1);
end
b=zeros(1,ms(1,4)+1);
for i=1:ms(1,4)+1
b(1,i)=A(i,i);
end
y=chase(a,b,c,f);
ans=zeros(5400/T+1,ms(1,4)+1); %结果矩阵
ans(1,:)=u0;
ans(2,:)=y;
%循环求结果
for i=2:5400/T
f=y';
f(1,1)=e*ue;
f(ms(1,1)+1,1)=0;
f(ms(1,2)+1,1)=0;
f(ms(1,3)+1,1)=0;
f(ms(1,4)+1,1)=us*u0;
y=chase(a,b,c,f);
ans(i+1,:)=y;
end
xlswrite('problem1.xlsx',ans,'Sheet2','A1');
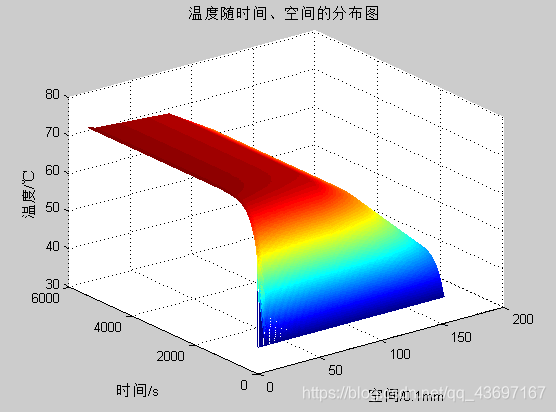
figure(1)
%温度随时间、空间的分布图
t=0:T:5400;
y=0:ms(1,4);
[b1,a1]=meshgrid(y,t);
mesh(b1,a1,ans);
title('温度随时间、空间的分布图');
%xlabel('空间/0.02mm');
xlabel('空间/0.1mm');
ylabel('时间/s');
zlabel('温度/℃');
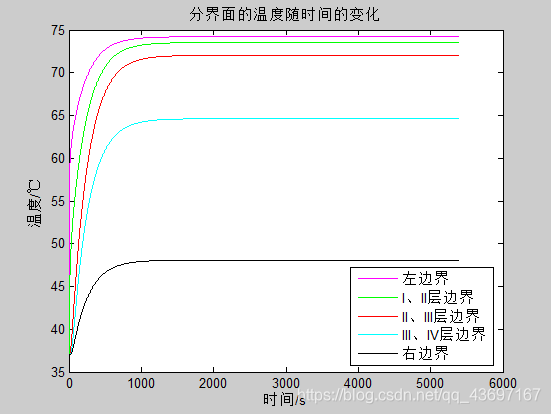
figure(2)
%分界面的温度随时间的变化图
t=0:T:5400;
%左边界
l1=ans(:,1);
%第一层和第二层边界
l2=ans(:,ms(1,1)+1);
%第二层和第三层边界
l3=ans(:,ms(1,2)+1);
%第三层和第四层边界
l4=ans(:,ms(1,3)+1);
%右边界I、II、III、IV
l5=ans(:,ms(1,4)+1);
plot(t,l1,'m-',t,l2,'g-',t,l3,'r-',t,l4,'c-',t,l5,'k-');
xlabel('时间/s');
ylabel('温度/℃');
title('分界面的温度随时间的变化');
legend('左边界','I、II层边界','II、III层边界','III、IV层边界','右边界');
%追赶法 chase.m
function x=chase(a,b,c,f)
%求解线性方程组 Ax=f, 其中 A是三对角阵
%a是矩阵 A的下对角线元素 a(1)=0
%b是矩阵 A的对角线元素
%c是矩阵 A的上对角线元素 c(n)=0
%f是方程组的右端向量
n=length(f);
x=zeros(1,n);
y=zeros(1,n);
d=zeros(1,n);
z= zeros(1,n);
%预处理
d(1)=b(1);
for i=1:n-1
z(i)=c(i)/d(i);
d(i+1)=b(i+1)-a(i+1)*z(i);
end
%追的过程
y(1)=f(1)/d(1);
for i=2:n
y(i)=(f(i)-a(i)*y(i-1))/d(i);
end
%赶的过程
x(n)=y(n);
for i=n-1:-1:1
x(i)=y(i)-z(i)*x(i+1);
end
% 求ke,ks quedingxishu.m
clc,clear;
a=load('TT.txt'); %TT.txt 存储的是附件2的所有数字信息
ue=75; %环境温度
us=37; %皮肤内测温度
ks=8.36; %与皮肤的热交换系数
keq=1;%最合适的 与环境的热交换系数
ksq=1;%最合适的 与皮肤的热交换系数
min=100000; %初始值
k=[0.082 0.37 0.045 0.028]; %热传导率
l=[0.6 6.6 10.2 15.2]*10^-3;
sum=l(1,1)/k(1,1);
for j=2:4
sum=sum+(l(1,j)-l(1,j-1))/k(1,j);
end
um=48.08; %稳态温度
time=a(:,2);
time=time';
for ks=7.8:0.02:8.8
ke=1/((ue-um)/(ks*(um-us))-sum); %与外界的热交换系数
w=ul4(ke,ks);
min1=0;
for i=1:5041
min1=min1+1/2*(time(1,i)-w(1,i))^2;
end
if min1<min
min=min1;
keq=ke;
ksq=ks;
end
end
min
keq %最合适的 与环境的热交换系数
ksq %最合适的 与皮肤的热交换系数
%问题1 返回稳态的温度用于求ke,ks的值 ul4.m
%问题1 返回稳态的温度用于求ke,ks ul4.m
function [q] = ul4( ke,ks )
T=1; %时间步长
m=[6 60 36 50];%将每一层细分为0.1mm每块
%m=[30 300 180 250] %将每一层细分为0.02mm每块
ms=[0 0 0 0]; % ms表示总的分层数
ms(1,1)=m(1,1);
for j=2:4
ms(1,j)=ms(1,j-1)+m(1,j);
end
l=[0.6 6.6 10.2 15.2]*10^(-3); %l1 l2 l3 l4z的坐标
p=[300 862 74.2 1.18]; %各层密度
c=[1377 2100 1726 1005]; %比热
k=[0.082 0.37 0.045 0.028]; %热传导率
u0=37.0; %初始温度
ue=75;
%求空间步长
x=zeros(1,4);
x(1,1)=l(1,1)/m(1,1);
for j=2:4
x(1,j)=(l(1,j)-l(1,j-1))/m(1,j);
end
% M(1,j) 从第1层到第j层的等分数
M(1,1)=m(1,1);
for j=2:4
M(1,j)=M(1,j-1)+m(1,j);
end
%求式（10）里的λ，用b表示λ
for j=1:4
b(1,j)=(k(1,j)*T)/(c(1,j)*p(1,j)*(x(1,j)^2));
end
e=(ke*x(1,1)/k(1,1)); %求式（12）的ue 用e表示
us=(ks*x(1,4)/k(1,4)); %求式（13）的us
for j=1:4
v(1,j)=k(1,j)/x(1,j); %求式（14）的v
end
u=zeros(5400/T+1,ms(1,4)+1); %建立一个以距离为x轴，时间为y轴的坐标轴
u(1,:)=37; %时间t=0时，各点温度为37度
f=zeros(ms(1,4)+1,1); %AX=f
x01=e+1; %l0的边界条件
x02=-1;
x1=[-b(1,1) 1+2*b(1,1) -b(1,1)]; %第一层
x2=[-b(1,2) 1+2*b(1,2) -b(1,2)]; %第二层
x3=[-b(1,3) 1+2*b(1,3) -b(1,3)]; %第三层
x4=[-b(1,4) 1+2*b(1,4) -b(1,4)]; %第四层
x12=[-v(1,1) v(1,1)+v(1,2) -v(1,2)]; %12层边界
x23=[-v(1,2) v(1,2)+v(1,3) -v(1,3)];%23层边界
x34=[-v(1,3) v(1,3)+v(1,4) -v(1,4)];%34层边界
x51=-1; %l4的边界条件
x52=1+us;
A=zeros(ms(1,4)+1,ms(1,4)+1);
A(1,1)=x01;
A(1,2)=x02;
f(1,1)=e*ue;
for i=2:ms(1,1)
A(i,i-1:i+1)=x1;
f(i,1)=37;
end
A(ms(1,1)+1,ms(1,1):ms(1,1)+2)=x12;
f(ms(1,1)+1,1)=0;
for i=ms(1,1)+2:ms(1,2)
A(i,i-1:i+1)=x2;
f(i,1)=37;
end
A(ms(1,2)+1,ms(1,2):ms(1,2)+2)=x23;
f(ms(1,2)+1,1)=0;
for i=ms(1,2)+2:ms(1,3)
A(i,i-1:i+1)=x3;
f(i,1)=37;
end
A(ms(1,3)+1,ms(1,3):ms(1,3)+2)=x34;
f(ms(1,3)+1,1)=0;
for i=ms(1,3)+2:ms(1,4)
A(i,i-1:i+1)=x4;
f(i,1)=37;
end
A(ms(1,4)+1,ms(1,4))=x51;
A(ms(1,4)+1,ms(1,4)+1)=x52;
f(ms(1,4)+1,1)=us*u0;
%追赶法
a=zeros(1,ms(1,4)+1);%下对角元素
a(1,1)=0;
for i=2:ms(1,4)+1
a(1,i)=A(i,i-1);
end
c=zeros(1,ms(1,4)+1);%上对角元素
c(1,ms(1,4)+1)=0;
for i=1:ms(1,4)
c(1,i)=A(i,i+1);
end
b=zeros(1,ms(1,4)+1);
for i=1:ms(1,4)+1
b(1,i)=A(i,i);
end
y=chase(a,b,c,f);
ans=zeros(5400/T+1,ms(1,4)+1); %结果矩阵
ans(1,:)=u0;
ans(2,:)=y;
%循环求结果
for i=2:5400/T
f=y';
f(1,1)=e*ue;
f(ms(1,1)+1,1)=0;
f(ms(1,2)+1,1)=0;
f(ms(1,3)+1,1)=0;
f(ms(1,4)+1,1)=us*u0;
y=chase(a,b,c,f);
ans(i+1,:)=y;
end
q=ans(:,ms(1,4)+1);
q=q';
end
问题（2）
%问题2的主函数 T2.m
clc,clear;
len=0.1; %二分法结束的条件
min=0.6;
max=25;
ans=0;%结果
q=fun2(min);%求解最小厚度情况下是否满足约束条件
if q(1,3601)<=47&&q(1,3301)<=44
ans=min;
fprintf('最小厚度情况下满足约束条件');
end
q=fun2(max);%求解最大厚度情况下是否满足约束条件
if q(1,3601)>47||q(1,3301)>44
fprintf('最大厚度情况下不满足约束条件,此题无解');
end
while(max-min>len)
mid=(min+max)/2;
q=fun2(mid);
if q(1,3601)<=47&&q(1,3301)<=44
max=mid;
else
min=mid;
end
end
ans=max
%对于不同的L2，返回皮肤外侧温度变化 fun2.m
function [q]=fun2(l2)
%l2 传入II层的厚度
T=1;%时间步长
s=ceil(l2/0.1);
m=zeros(1,4);
%将每一层细分为0.1mm每块
m(1,1)=6;
m(1,2)=s;
m(1,3)=36;
m(1,4)=55;
ms=[0 0 0 0]; % ms表示总的分层数
ms(1,1)=m(1,1);
for j=2:4
ms(1,j)=ms(1,j-1)+m(1,j);
end
l=[0.6 l2+0.6 l2+4.2 l2+9.7]*10^(-3); %l1 l2 l3 l4的坐标
p=[300 862 74.2 1.18]; %各层密度
c=[1377 2100 1726 1005]; %比热
k=[0.082 0.37 0.045 0.028]; %热传导率
u0=37.0; %初始温度
ue=65; %环境温度
%求空间步长
x=zeros(1,4);
x(1,1)=l(1,1)/m(1,1);
for j=2:4
x(1,j)=(l(1,j)-l(1,j-1))/m(1,j);
end
% M(1,j) 从第1层到第j层的等分数
M(1,1)=m(1,1);
for j=2:4
M(1,j)=M(1,j-1)+m(1,j);
end
%求式（10）里的λ，用b表示λ
for j=1:4
b(1,j)=(k(1,j)*T)/(c(1,j)*p(1,j)*(x(1,j)^2));
end
ke=117.4035;
e=(ke*x(1,1)/k(1,1)); %求式（12）的ue 用e表示
ks=8.36;
us=(ks*x(1,4)/k(1,4)); %求式（13）的us
for j=1:4
v(1,j)=k(1,j)/x(1,j); %求式（14）的v
end
u=zeros(5400/T+1,ms(1,4)+1); %建立一个以距离为x轴，时间为y轴的坐标轴
u(1,:)=37; %时间t=0时，各点温度为37度
f=zeros(ms(1,4)+1,1); %AX=f
x01=e+1; %l0的边界条件
x02=-1;
x1=[-b(1,1) 1+2*b(1,1) -b(1,1)]; %第一层
x2=[-b(1,2) 1+2*b(1,2) -b(1,2)]; %第二层
x3=[-b(1,3) 1+2*b(1,3) -b(1,3)]; %第三层
x4=[-b(1,4) 1+2*b(1,4) -b(1,4)]; %第四层
x12=[-v(1,1) v(1,1)+v(1,2) -v(1,2)]; %12层边界
x23=[-v(1,2) v(1,2)+v(1,3) -v(1,3)];%23层边界
x34=[-v(1,3) v(1,3)+v(1,4) -v(1,4)];%34层边界
x51=-1; %l4的边界条件
x52=1+us;
A=zeros(ms(1,4)+1,ms(1,4)+1);
A(1,1)=x01;
A(1,2)=x02;
f(1,1)=e*ue;
for i=2:ms(1,1)
A(i,i-1:i+1)=x1;
f(i,1)=37;
end
A(ms(1,1)+1,ms(1,1):ms(1,1)+2)=x12;
f(ms(1,1)+1,1)=0;
for i=ms(1,1)+2:ms(1,2)
A(i,i-1:i+1)=x2;
f(i,1)=37;
end
A(ms(1,2)+1,ms(1,2):ms(1,2)+2)=x23;
f(ms(1,2)+1,1)=0;
for i=ms(1,2)+2:ms(1,3)
A(i,i-1:i+1)=x3;
f(i,1)=37;
end
A(ms(1,3)+1,ms(1,3):ms(1,3)+2)=x34;
f(ms(1,3)+1,1)=0;
for i=ms(1,3)+2:ms(1,4)
A(i,i-1:i+1)=x4;
f(i,1)=37;
end
A(ms(1,4)+1,ms(1,4))=x51;
A(ms(1,4)+1,ms(1,4)+1)=x52;
f(ms(1,4)+1,1)=us*u0;
%追赶法
a=zeros(1,ms(1,4)+1);%下对角元素
a(1,1)=0;
for i=2:ms(1,4)+1
a(1,i)=A(i,i-1);
end
c=zeros(1,ms(1,4)+1);%上对角元素
c(1,ms(1,4)+1)=0;
for i=1:ms(1,4)
c(1,i)=A(i,i+1);
end
b=zeros(1,ms(1,4)+1);
for i=1:ms(1,4)+1
b(1,i)=A(i,i);
end
y=chase(a,b,c,f);
ans=zeros(5400/T+1,ms(1,4)+1); %结果矩阵
ans(1,:)=u0;
ans(2,:)=y;
%循环求结果
for i=2:5400/T
f=y';
f(1,1)=e*ue;
f(ms(1,1)+1,1)=0;
f(ms(1,2)+1,1)=0;
f(ms(1,3)+1,1)=0;
f(ms(1,4)+1,1)=us*u0;
y=chase(a,b,c,f);
ans(i+1,:)=y;
end
q=ans(:,ms(1,4)+1);
q=q';
end
%求假人皮肤外侧稳定温度随II层厚度的变化 draw.m
clc,clear;
i=0;
for l2=0.6:0.1:25
q=fun2(l2);
i=i+1;
a(1,i)=q(1,length(q));
end
l2=0.6:0.1:25;
plot(l2,a,'c');
title('假人皮肤外侧稳定温度随II层厚度的变化');
xlabel('II层厚度/mm');
ylabel('假人皮肤外侧稳定温度/摄氏度');
问题(3)
%问题3的主函数 T3.m
clc,clear;
len=0.1; %二分法结束的条件
min=0.6;
max=25;
ans=0;%结果
q=fun3(min);%求解最小厚度情况下是否满足约束条件
if q(1,1801)<=47&&q(1,1501)<=44
ans=min;
fprintf('最小厚度情况下满足约束条件');
end
q=fun3(max);%求解最大厚度情况下是否满足约束条件
if q(1,1801)>47||q(1,1501)>44
fprintf('最大厚度情况下不满足约束条件,此题无解');
end
while(max-min>len)
mid=(min+max)/2;
q=fun3(mid);
if q(1,1801)<=47&&q(1,1501)<=44
max=mid;
else
min=mid;
end
end
ans=max
%传入不同的L2,返回皮肤外侧的温度变化矩阵 fun3.m
function [q]=fun3(l2)
%l2 传入II层的厚度
T=1;%时间步长
s=ceil(l2/0.1);
m=zeros(1,4);
%将每一层细分为0.1mm每块
m(1,1)=6;
m(1,2)=s;
m(1,3)=36;
m(1,4)=64; %第四层取6.4mm
ms=[0 0 0 0]; % ms表示总的分层数
ms(1,1)=m(1,1);
for j=2:4
ms(1,j)=ms(1,j-1)+m(1,j);
end
l=[0.6 l2+0.6 l2+4.2 l2+10.6]*10^(-3); %l1 l2 l3 l4的坐标
p=[300 862 74.2 1.18]; %各层密度
c=[1377 2100 1726 1005]; %比热
k=[0.082 0.37 0.045 0.028]; %热传导率
u0=37.0; %初始温度
ue=80; %环境温度
%求空间步长
x=zeros(1,4);
x(1,1)=l(1,1)/m(1,1);
for j=2:4
x(1,j)=(l(1,j)-l(1,j-1))/m(1,j);
end
% M(1,j) 从第1层到第j层的等分数
M(1,1)=m(1,1);
for j=2:4
M(1,j)=M(1,j-1)+m(1,j);
end
%求式（10）里的λ，用b表示λ
for j=1:4
b(1,j)=(k(1,j)*T)/(c(1,j)*p(1,j)*(x(1,j)^2));
end
ke=117.4035;
e=(ke*x(1,1)/k(1,1)); %求式（12）的ue 用e表示
ks=8.36;
us=(ks*x(1,4)/k(1,4)); %求式（13）的us
for j=1:4
v(1,j)=k(1,j)/x(1,j); %求式（14）的v
end
u=zeros(5400/T+1,ms(1,4)+1); %建立一个以距离为x轴，时间为y轴的坐标轴
u(1,:)=37; %时间t=0时，各点温度为37度
f=zeros(ms(1,4)+1,1); %AX=f
x01=e+1; %l0的边界条件
x02=-1;
x1=[-b(1,1) 1+2*b(1,1) -b(1,1)]; %第一层
x2=[-b(1,2) 1+2*b(1,2) -b(1,2)]; %第二层
x3=[-b(1,3) 1+2*b(1,3) -b(1,3)]; %第三层
x4=[-b(1,4) 1+2*b(1,4) -b(1,4)]; %第四层
x12=[-v(1,1) v(1,1)+v(1,2) -v(1,2)]; %12层边界
x23=[-v(1,2) v(1,2)+v(1,3) -v(1,3)];%23层边界
x34=[-v(1,3) v(1,3)+v(1,4) -v(1,4)];%34层边界
x51=-1; %l4的边界条件
x52=1+us;
A=zeros(ms(1,4)+1,ms(1,4)+1);
A(1,1)=x01;
A(1,2)=x02;
f(1,1)=e*ue;
for i=2:ms(1,1)
A(i,i-1:i+1)=x1;
f(i,1)=37;
end
A(ms(1,1)+1,ms(1,1):ms(1,1)+2)=x12;
f(ms(1,1)+1,1)=0;
for i=ms(1,1)+2:ms(1,2)
A(i,i-1:i+1)=x2;
f(i,1)=37;
end
A(ms(1,2)+1,ms(1,2):ms(1,2)+2)=x23;
f(ms(1,2)+1,1)=0;
for i=ms(1,2)+2:ms(1,3)
A(i,i-1:i+1)=x3;
f(i,1)=37;
end
A(ms(1,3)+1,ms(1,3):ms(1,3)+2)=x34;
f(ms(1,3)+1,1)=0;
for i=ms(1,3)+2:ms(1,4)
A(i,i-1:i+1)=x4;
f(i,1)=37;
end
A(ms(1,4)+1,ms(1,4))=x51;
A(ms(1,4)+1,ms(1,4)+1)=x52;
f(ms(1,4)+1,1)=us*u0;
%追赶法
a=zeros(1,ms(1,4)+1);%下对角元素
a(1,1)=0;
for i=2:ms(1,4)+1
a(1,i)=A(i,i-1);
end
c=zeros(1,ms(1,4)+1);%上对角元素
c(1,ms(1,4)+1)=0;
for i=1:ms(1,4)
c(1,i)=A(i,i+1);
end
b=zeros(1,ms(1,4)+1);
for i=1:ms(1,4)+1
b(1,i)=A(i,i);
end
y=chase(a,b,c,f);
ans=zeros(5400/T+1,ms(1,4)+1); %结果矩阵
ans(1,:)=u0;
ans(2,:)=y;
%循环求结果
for i=2:5400/T
f=y';
f(1,1)=e*ue;
f(ms(1,1)+1,1)=0;
f(ms(1,2)+1,1)=0;
f(ms(1,3)+1,1)=0;
f(ms(1,4)+1,1)=us*u0;
y=chase(a,b,c,f);
ans(i+1,:)=y;
end
q=ans(:,ms(1,4)+1);
q=q';
end
代码都是自己花时间码出来的，问题应该是没有的，不足就是重复性比较高。非常感谢大家的关注与提问，因本题是2018国赛的题目，网上的优秀论文也比较多，花个几天时间去理解，算法也比较容易实现。因为作者在准备考研，时间比较紧张，不能及时回复大家，还请多多见谅。
作者有幸参加了2019年高教社杯数学建模，运气比较好，获得了湖南省一等奖、全国二等奖的成绩，就自己最大的感受而言，抛开团队及其他因素，前期的积淀是比较重要的，数学建模算法及应用这本书大部分内容要去弄懂，代码尽量去实现，如果学校有培训，尽量去参加，不要划水，我所了解到的划水的最后至多得了个省二省三，该付出时间的你一个都跑不掉。今年国赛我也报名了，希望我和各位都能取得一个满意的成绩。
扫一扫
680
到【灌水乐园】发言
