论文笔记——GNN3DMOT: Graph Neural Network for 3D Multi-Object Tracking with 2D-3D Multi-Feature Learning

**模型管道：**tracking-by-detection，这种管道性能主要受目标检测质量和鉴别特征学习两个因素的影响。
工作：
1、提出了一种新的特征提取器，可以从二维空间联合学习运动和三维空间的运动和外观特征。
2、遵循Dropout的概念，并提出了一个集成训练范式，允许网络在训练过程中随机关闭分支。因此，网络可以学习所有分支上的鉴别特征。
3、提出了一种使用GNN的特征交互机制，用于学习区别度高的特征。

目前研究现状：
虽然gnn在许多领域都表现出了良好的性能，但目前还没有将gnn应用于MOT的工作。本篇论文第一次尝试使用gnn进行在线MOT。

3D Appearance/Motion Feature Extraction.
3D Appearance Feature Extraction：使用激光雷达点云作为外观提示。首先提取三维检测盒包围的点云，然后应用PointNet获得该特征。

3D Motion Feature Extraction：作者直接使用三维检测盒作为运动信号。请注意，作者使用不同的三维运动特征提取器来跟踪和检测到的对象，因为被跟踪的对象在过去的帧中有相关的轨迹，而检测到的对象没有。对于跟踪对象，作者使用LSTM融合过去T帧的运动信息。对于检测到的对象，作者使用一个2层MLP（多层感知器），以t+1帧中的检测作为输入来提取特征。

2D Appearance/Motion Feature Extraction.
2D Appearance Freature Extraction:使用图像补丁作为外观信号（根据二维检测从整个图像中裁剪出来）。为了处理图像补丁并获得二维外观特征，作者使用了CNN(例如，VGGNet或ResNet)

2D Montion Feature Extraction:同3D Motion Feature Extraction，但是使用的坐标不一样。

Feature Fusion
作者尝试了两种不同的融合方式：（1）将二维和三维特征拼接在一起；（2）将二维和三维特征元素相加在一起。最终采用了第一种方式。

Graph Neural Network for Data Association
特征融合后，对t帧跟踪的对象有M个特征，对t+1帧检测到的对象有N个特征。总的来说，图中有M+N节点，所示图中的边。一种简单的方法是在每对节点之间都有一条边，这就得到了一个全连通的图，而且计算成本可能很昂贵。作者没有使用这个简单的边缘构造，而是使用了关于在线MOT的先验知识，其中匹配应该只发生在不同的帧之间（即，而不是在同一帧内）。此外，对于第t帧中的任何跟踪对象在t+1中可能匹配的检测很可能位于附近位置。因此，作者只构造了两个节点的检测中心在二维三维空间中的距离小于固定值的边。因此，在最终的网络中存在一个跨帧的稀疏边连接。

Edge Regression
为了求解在线MOT问题，我们需要根据t帧中M跟踪对象和t+1中N检测对象的特征的两两相似性计算M×N亲和矩阵A。在GNN的背景下，作者将这个过程称为边缘回归。
作者尝试了三个度量标准来衡量特征的相似度。前两个是余弦相似度和负l2距离，这是MOT社区中使用的传统度量标准。第三种方法是采用一个两层MLP，以两个节点特征的差值作为输入，并输出一个在0到1之间的标量值作为成对相似度得分。最终作者使用MLP作为边缘回归的度量标准。

Node Feature Aggregation
为了建模GNN中的特征交互，作者通过聚合GNN每一层的邻域（即通过边缘连接的节点）的特征来迭代更新节点特征。
作者尝试了四种不同的聚合方式，并且尝试了不同的图卷积层数。四种不同的聚合方式如下：

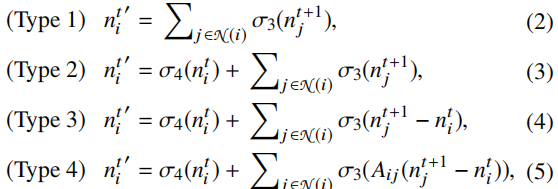
Losses
我们提出的网络在训练过程中对所有K层使用两个损失：（1）批三重损失Ltri；（2）亲和损失Laff。我们可以将整个损失函数L总结如下：

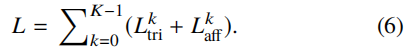
Batch Triplet Loss
为了学习匹配的鉴别特征，首先在GNN层的每一层的节点特征都应用三元组损失。 For node nti that has a matched node ntj+1（即，对象oi与dj具有相同的ID），每个层中的三元组损失定义为：

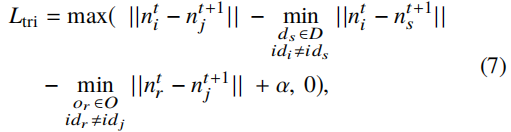
Affinity Loss
除了应用于节点特征的批处理三联体损失外，我们还使用了一个亲和损失Laff来直接监督网络的最终输出，即预测的亲和矩阵a。我们的亲和性损失包括两个单独的损失。
首先，我们知道真亲和矩阵Ag在所有的元素上只有整数0或1，我们可以将亲和矩阵的预测表示为一个二值分类问题。因此，我们的第一个损二分类交叉熵损失Lbce应用于预测矩阵A中的每个元素，如下所示：

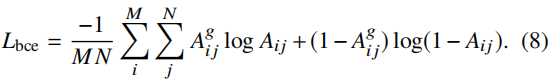
此外，我们知道在t帧中的每个跟踪对象oti只能有一个匹配的检测dtj+1，或者根本没有匹配。换句话说，Ag的每一行和列只能是一个热向量（即，在单个项中有1，在所有其他项中包含0的向量）或一个全零向量。由此可以定义亲和矩阵的第二个损失。对于Ag中所有有一个热向量的行和列，我们将交叉熵损失Lce应用于A中的相应行和列。如下图所示，真实亲和矩阵中的Ag·j列为单热向量，第j列的损失Lce定义为：

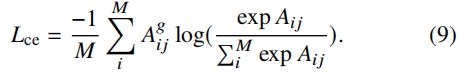
我们现在可以总结亲和损失如下：