一、微积分进阶
1. 泰勒展开与多元泰勒公式
- 公式:
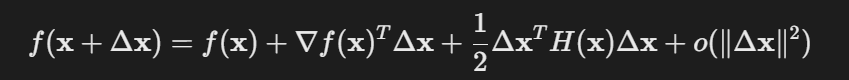
- 变量:
- ∇f:梯度向量,H:Hessian矩阵,Δx:增量向量。
- 应用:
- 牛顿法优化:二阶近似加速收敛(如逻辑回归的Hessian矩阵优化)。
- 函数近似:局部线性化非线性模型(如高斯过程回归)。
- 变量:
2. 多重积分与概率密度积分
- 公式:
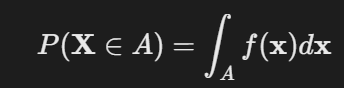
- 变量:
- f(x):联合概率密度函数,
 :积分区域。
:积分区域。
- f(x):联合概率密度函数,
- 应用:
- 贝叶斯推断:计算边缘概率
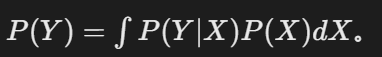
- 高斯过程:高维积分计算后验分布。
- 贝叶斯推断:计算边缘概率
- 变量:
二、实分析与测度论
1. 测度与积分(勒贝格积分)
- 公式:
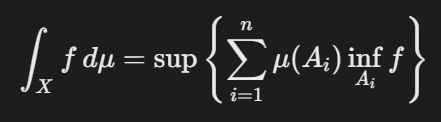
- 变量:
- μ:测度,Ai:可测集划分,f:可测函数。
- 应用:
- 概率公理化:概率空间 (Ω,F,P) 中的测度 P。
- 期望计算:
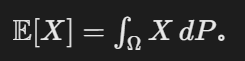
- 变量:
2. Radon-Nikodym定理
- 公式:
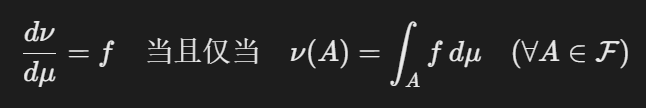
- 变量:
- ν,μ:测度,f:Radon-Nikodym导数。
- 应用:
- 概率密度比:重要性采样中的权重计算(如变分推断)。
- 变量:
三、泛函分析
1. 巴拿赫空间与希尔伯特空间
- 定义:
- 巴拿赫空间:完备的赋范线性空间(如 Lp 空间)。
- 希尔伯特空间:带有内积的完备空间(如 L2 空间)。
- 应用:
- 核方法(SVM):通过核技巧将数据映射到高维希尔伯特空间。
- 函数逼近:神经网络作为函数空间的逼近器。
2. 再生核希尔伯特空间(RKHS)
- 公式:
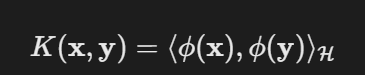
- 变量:
- K:核函数,ϕ:映射到RKHS的函数。
- 应用:
- 高斯过程:协方差函数定义在RKHS中。
- 支持向量机(SVM):非线性分类通过核函数隐式映射。
- 变量:
四、拓扑学与微分几何
1. 流形(Manifold)
- 定义:局部欧几里得空间的可微拓扑空间。
- 示例:
- 球面:二维流形嵌入三维空间。
- 图像数据流形:高维图像在低维流形上的分布。
- 应用:
- 流形学习:Isomap、LLE、t-SNE等降维算法。
- 生成模型:VAE在潜在空间假设数据服从流形结构。
2. 切空间与余切空间
- 公式:

- 变量:
- TpM:点 p 处的切空间,γ:过 p 的曲线。
- 应用:
- 优化:黎曼梯度下降在流形上的参数更新。
- 计算机视觉:3D姿态估计在SO(3)流形上的优化。
- 变量:
3. 曲率与黎曼几何
- 公式:
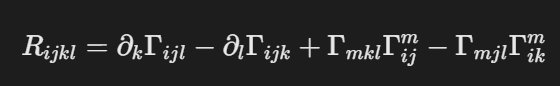
- 变量:
- 应用:
- 几何深度学习:图神经网络中引入曲率信息。
- 变量:
五、优化理论进阶
1. 凸优化与对偶理论
- 公式:
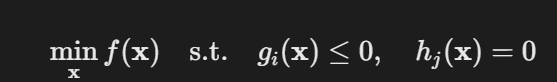
- 对偶问题:
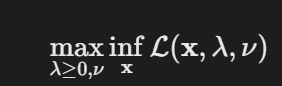
- 应用:
- SVM对偶问题:将原问题转化为高效求解的对偶形式。
- KKT条件:约束优化问题的最优性验证。
- 对偶问题:
2. 随机优化(Stochastic Optimization)
- 公式:
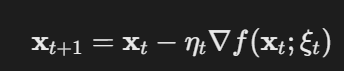
- 变量:
- ξt:随机采样的小批量数据,ηt:学习率。
- 应用:
- 深度学习:SGD及其变种(Adam、RMSProp)。
- 在线学习:实时更新模型参数。
- 变量:
六、测度论与概率论进阶
1. 大数定律与中心极限定理
- 大数定律:
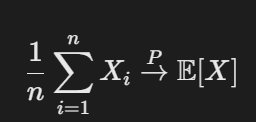
- 应用:
- 蒙特卡洛积分:用样本均值近似期望。
- 应用:
- 中心极限定理:
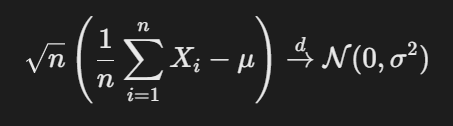
- 应用:
- 假设检验:置信区间与p值计算。
- 应用:
2. 随机过程
- 布朗运动(Wiener过程):
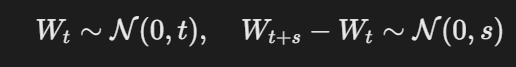
- 应用:
- 金融模型:Black-Scholes期权定价。
- 扩散模型:Stable Diffusion中的去噪过程。
- 应用:
七、张量分析与高阶代数
1. 张量积与多维数组
- 公式:

- 应用:
- Transformer模型:自注意力机制中的查询-键-值张量运算。
- 推荐系统:高阶张量分解(CP分解、Tucker分解)。
- 应用:
2. 张量网络(Tensor Network)
- 矩阵乘积态(MPS):
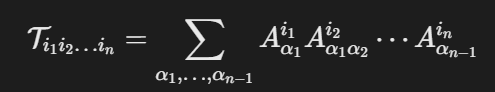
- 应用:
- 量子机器学习:量子态的张量网络表示。
- 压缩表示:高维数据的低秩近似。
- 应用:
八、李群与李代数
1. 旋转群SO(3)与SE(3)
- 定义:
- SO(3):三维旋转矩阵群
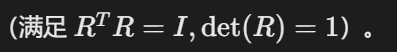 。
。 - SE(3):三维刚体变换群(旋转+平移)。
- SO(3):三维旋转矩阵群
- 应用:
- 机器人学:姿态估计与运动规划。
- 计算机视觉:多视角几何中的相机位姿优化。
2. 指数映射与对数映射
- 公式:

- 变量:
- so(3):李代数(反对称矩阵空间)。
- 应用:
- 姿态插值:在李代数空间中做线性插值后映射到李群。
- 变量:
九、范畴论(Category Theory)
1. 函子与自然变换
- 定义:
- 范畴:对象(Objects)与态射(Morphisms)的集合。
- 函子:范畴间的结构保持映射。
- 应用:
- 函数式编程:Monad在概率编程中的应用(如概率分布组合)。
- 类型理论:抽象模型的结构化表示。
2. 幺半范畴(Monoidal Category)
- 定义:带有张量积操作的范畴。
- 应用:
- 量子计算:量子门与量子线路的组合。
- 自然语言处理:词汇语义的组合性建模。
十、代数几何与交换代数
1. 代数簇(Algebraic Variety)
- 定义:多项式方程组的解集。
- 示例:
- 圆:由方程
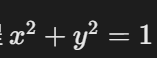 定义的代数簇。
定义的代数簇。
- 圆:由方程
- 应用:
- 密码学:椭圆曲线密码学(ECC)中的代数结构。
- 代数统计学:隐变量模型的参数空间分析。
2. 格罗滕迪克拓扑(Grothendieck Topology)
- 定义:范畴上的广义覆盖结构。
- 应用:
- 形式化数学:数学定理的机器证明(如Coq、Lean)。
十一、算子理论与谱分析
1. 线性算子与谱定理
- 公式:

- 变量:
- A:线性算子,λ:特征值,ψ:特征函数。
- 应用:
- 量子力学:哈密顿算子的能级分析。
- 主成分分析(PCA):协方差矩阵的谱分解。
- 变量:
2. 紧算子与希尔伯特-施密特算子
- 定义:
- 紧算子:将有界集映射到相对紧集。
- 希尔伯特-施密特算子:具有有限Hilbert-Schmidt范数的算子。
- 应用:
- 积分方程:核方法中的积分算子理论。
十二、非标准分析(Non-standard Analysis)
1. 超实数与无穷小量
- 定义:包含无穷小(ϵ)和无穷大(ω)的数域 ∗R。
- 应用:
- 物理建模:简化连续介质力学中的极限过程。
- 自动微分:利用双数(Dual Numbers)高效计算导数。
十三、总结与模型对应表
| 数学分支 | 应用模型与场景 |
|---|---|
| 泰勒展开 | 牛顿法优化、高斯过程回归 |
| 勒贝格积分 | 贝叶斯推断中的边缘化积分 |
| 泛函分析(RKHS) | 支持向量机(SVM)、高斯过程 |
| 微分几何(流形) | 流形学习(Isomap、LLE)、生成模型(VAE) |
| 李群与李代数 | 机器人运动学、3D视觉中的姿态估计 |
| 张量分析 | Transformer模型、推荐系统的张量分解 |
| 范畴论 | 函数式编程、量子计算中的组合逻辑 |
| 代数几何 | 椭圆曲线密码学、代数统计学 |
| 非标准分析 | 自动微分、物理建模中的无穷小分析 |
| 测度论(Radon-Nikodym) | 变分推断、重要性采样 |
| 算子理论 | 量子机器学习、核方法的理论支持 |























 24
24

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








