BP算法基础与实现

1，内容简介
BP算法（backpropagation,反向传播算法）的学习过程，由信息的正向传播和误差的反向传播两个过程组成。输入层各神经元介绍来自外界的输入信息，并传递给中间层各神经元。中间层是内部信息处理层，负责信息变换，根据信息变化能力的需求，中间层可以设计为单隐层或多隐层结构。最后一个隐层传递到输出层各神经元的信息，经过进一步处理后，完成一次正向的传播过程，由输出层向外界输出信息处理的结果。当实际输出与期望输出不同时，进入误差的反向传播阶段。误差通过输出层。按误差梯度下降的方式修正各层权值，向隐层、输入层、逐层反传。周而复始的信息正向传播和误差反向传播过程，是各层权值不断调整的过程，也是神经网络学习训练的过程，此过程一直进行到网络输出的误差减少到可以接受的程度或者预先设定的学习次数为止。
2，理论推导
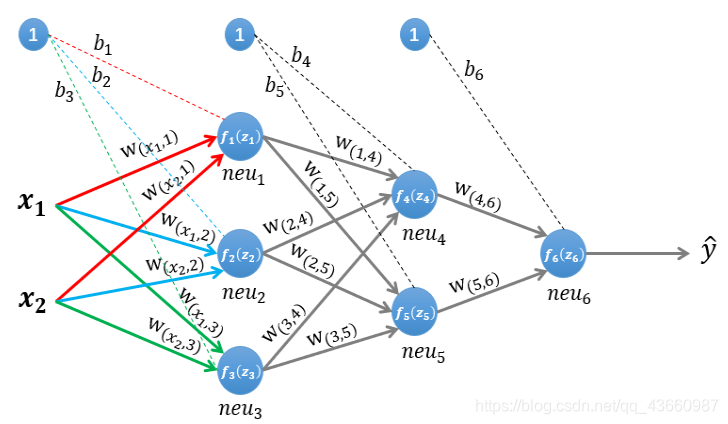
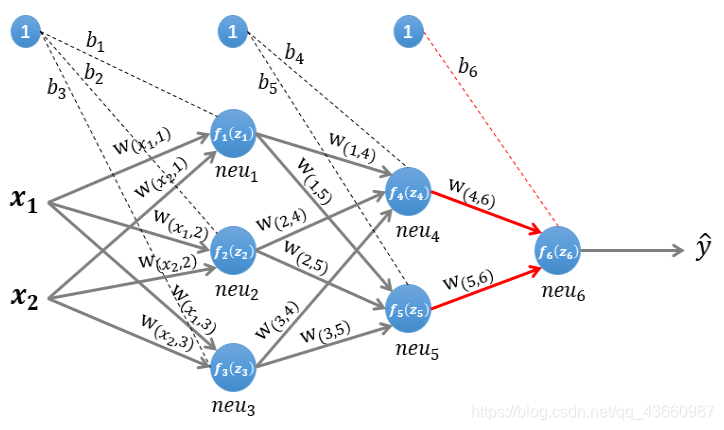
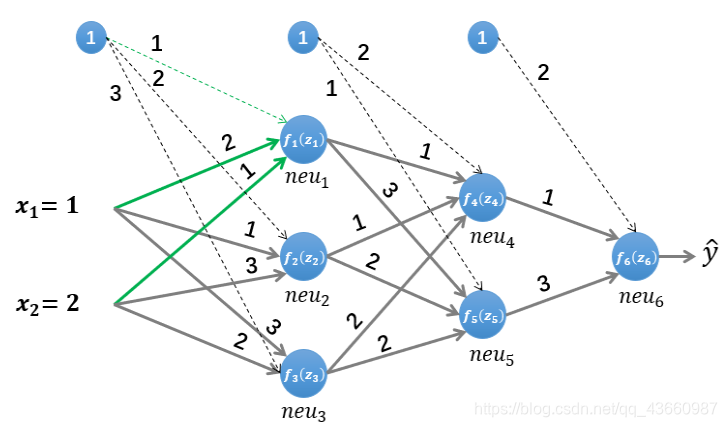
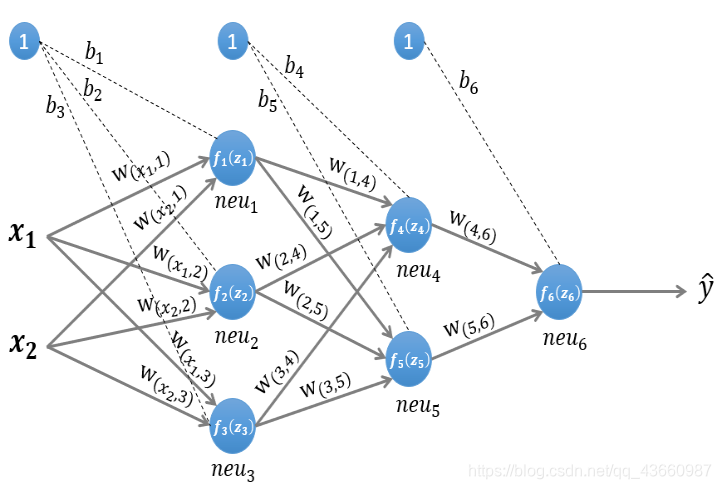上图是一个简单的三层（两个隐藏层，一个输出层）神经网络结构，假设使用这个神经网络来解决二分类问题，给这个网络一个输入样本（x1，x2） ，通过前向运算得到输出 。输出值 的值域为[0,1] ，例如 y的值越接近0，代表该样本是“0”类的可能性越大，反之是“1”类的可能性大
2.1 前向传播
为了便于理解后续的内容，需要先搞清楚前向传播的计算过程，以上图所示的内容为例，输入的样本为：

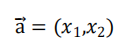
第一层网络的参数为：

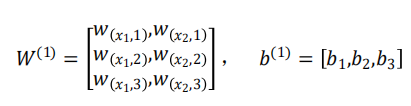
第二层网络的参数为：

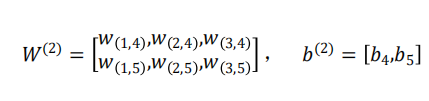
第三层网络的参数为：

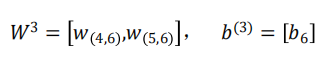
2.1.1 第一层隐藏层的计算
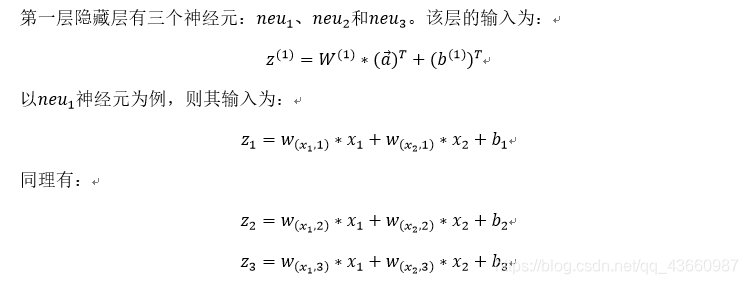
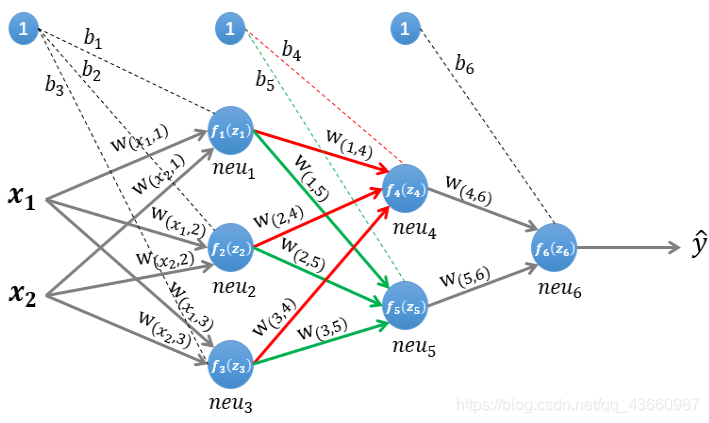
2.1.2第二层隐藏层的计算
2.1.3输出层的计算
输出只有一个神经元neu6，该层的输入为：

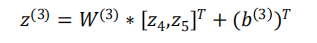
即：

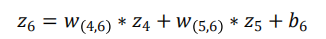
因为该网络要解决二分类问题，所以输出层的激活函数也可以用一个Sigmoid型函数，神经网络最后的输出为f6（z6）.
2.1 反向传播
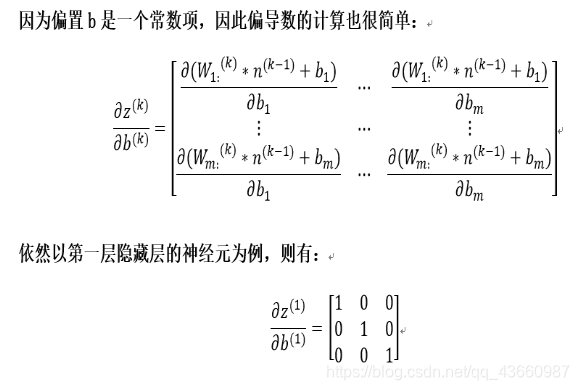
2.2 计算偏导数
下面将实际数据代入上面的网络模型中：

我们上面提到的简单的神经网络，其中所有参数的初始值如下：
输入的样本为（假设其真实类标为“1”）：

第一层网络的参数为：
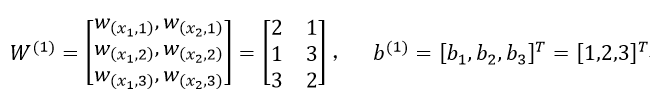第二层网络的参数为：
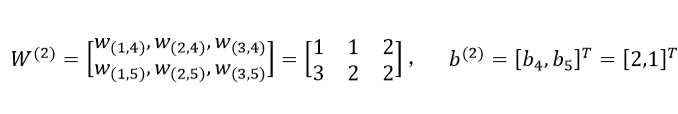第三层网络的参数为：

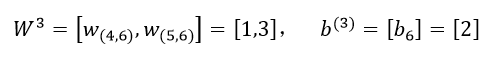
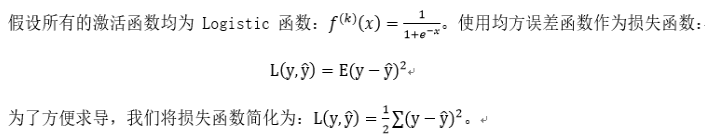前向传播：
我们首先初始化神经网络的参数，计算第一层神经元：
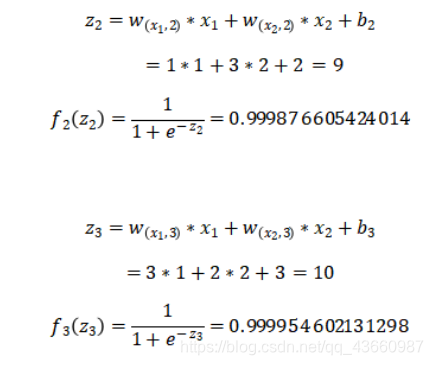
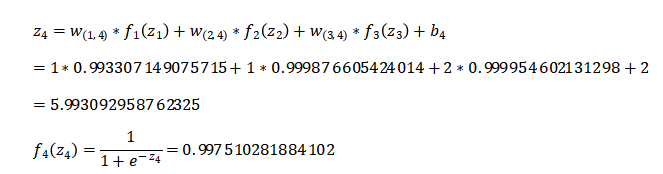误差反向传播：
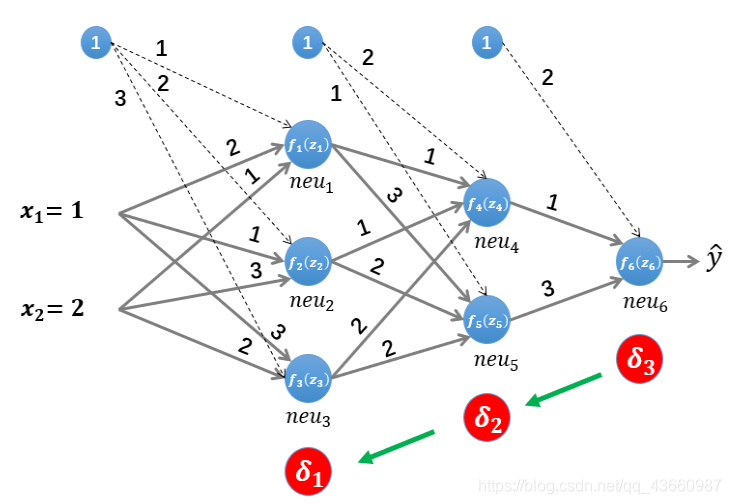
接着计算第二层隐藏层的误差项，根据误差项的计算公式有：
最后是计算第一层隐藏层的误差项：
更新参数：
上一小节中我们已经计算出了每一层的误差项，现在我们要利用每一层的误差项和梯度来更新每一层的参数，权重W和偏置b的更新公式如下：

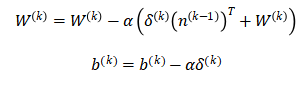
通常权重W的更新会加上一个正则化项来避免过拟合，这里为了简化计算，我们省去了正则化项。上式中的a 是学习率，我们设其值为0.1。参数更新的计算相对简单，每一层的计算方式都相同，因此仅演示第一层隐藏层的参数更新：
至此，我们已经完整介绍了BP算法的原理，并使用具体的数值做了计算示例。
参考博文地址：https://blog.youkuaiyun.com/fendouaini/article/details/79789440