dp一维数组和二维数组如何追踪路径

       刚开始学dp，学的是01背包，讲过两种方法，一种是开一个二维数组dp可以追踪路径，因为所有的dp都记录着，第二种方法是开一维数组，但是dp的值会被不断覆盖，没有办法从dp中找到之前走的路。但是会大大的改善空间和时间的复杂度。但是今天，要讲一个一维数组追踪路径的办法。

二维数组追踪法

之前看了一个博客讲的很清楚，可以去看一下这部分：https://blog.youkuaiyun.com/xp731574722/article/details/70766804

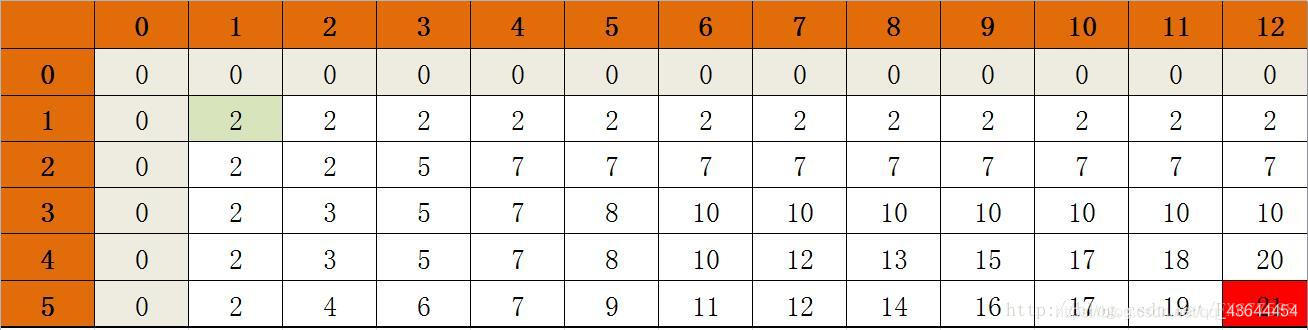
可以从图中看出所走的路。

void traceback()
{
    for(int i=n; i>1; i--)
    {
        if(dp[i][c]==dp[i-1][c])   //根据公式判断他等于上一步的哪个值。          
            x[i]=0;  //x[i]=0表示没有走过，x[i]=1表示走过。
        else
        {
            x[i]=1;
            c-=w[i];
        }
    }
    x[1]=(m[1][c]>0)?1:0;
}

**一维数组**
由于一维数组中的数值已经被重新赋值，无法追踪，所以我们要开一个数组，在每次得到dp时，将上一步的下标记录下来。
 

 dp[i]=dp[j]+1;  //这里给的是简单的公式，如果是max选择，要判断取得是哪个值，然后记录所取值得下标
    l[i]=j;

 然后就很奇妙了