k-means算法python（详细注释）

我只是加了更多的注释，详细过程参考下面的这篇博文：

参考博文链接.

代码：

# -*- coding: utf-8 -*-
# import numpy as np    使用numpy里面的函数时，需要在前面加np.
from numpy import *     # 导入numpy的库函数

# 加载数据集
def loadDataSet(fileName):
    dataMat = []
    fr = open(fileName)
    """
     fileName:是包含了访问的文件名称的路径字符串
     open（）返回一个file对象
    """
    for line in fr.readlines():
        """
                strip()将line行开头和结尾的空白符号删掉。split('\t') 函数以‘\t’为切分符号对每行切分
                split函数返回的结果是一个列表，赋值给curLine 
         """
        curLine = line.strip().split('\t')
        """#map()是 Python 内置的高阶函数，它接收一个函数 f 和一个 list，
               并通过把函数 f 依次作用在 list 的每个元素上，得到一个新的 list 并返回。
        """
        fltLine =list(map(float, curLine))
        '''
        map()是将curline的元素转化为float，然后返回迭代器，再转化为list
        '''
        dataMat.append(fltLine) # 把fltline加入到datamat
    return dataMat

# 欧几里得距离
def countDist(vecA, vecB):
    return sqrt(sum(power(vecA - vecB, 2)))

# 随机产生中心
def randCent(dataSet, k):
    n = shape(dataSet)[1] # 计算dataset的规模后返回列数
    centroids = mat(zeros([k, n]))  # 初始化一个k行n列的二维数组，数组初始值全部为0，然后用mat函数将其转化为矩阵
    for j in range(n):
        minj = min(dataSet[:, j])   # 找第j列的最小值
        rangej = float(max(dataSet[:, j]) - minj)   # 找第j列的最大值后减去最小值，转化为浮点型
        centroids[:, j] = mat(minj + rangej * random.rand(k, 1))
        '''
        random.rand()产生0-1之间的数
        random.rand(k, 1)产生k行一列
        minj + rangej * random.rand()，产生一个数，最小产生0，相乘后还是0，加上最小的；
        最大为1相乘后得到rangej，加上minj，就相当于得到l一个最大值，之前减去过一个minj
        mat（）矩阵化
        '''
    return centroids

# k-means算法
def kMeans(dataSet, k, distMeas=countDist, createCent=randCent):
    # 将函数distEclud和randCent作为参数传进来，可以更好的封装kMeans函数
    print(shape(dataSet))
    m = shape(dataSet)[0]   # 计算dataset的规模，返回行数
    """ clusterAssment是一个m行2列的矩阵，第一列存放每个样本所属聚类中心的下标，
            第二列存放该样本与该聚类中心的距离
     """
    clusterAssment = mat(zeros((m, 2))) # 产生为0的m×2的元组转化为矩阵
    centroids = createCent(dataSet, k)  # 随机产生中心
    clusterChanged = True       # 设置初始值
    while clusterChanged:
        clusterChanged = False  # 首先设置为false让他可以结束循环，在后面的计算中，如果中心的坐标发生变化，某一点的所属类发现变化就要继续循环
        # 下面两个for循环计算每一个样本到每一个聚类中心的距离
        for i in range(m):  # 遍历样本
            minDist = inf   # inf表示无穷大，-inf表示无穷小
            minIndex = -1
            for j in range(k):  #遍历聚类中心
                distJI = distMeas(centroids[j, :], dataSet[i, :])   # 计算距离
                if distJI < minDist:    #规划到距离最小的那一类
                    minDist = distJI;
                    minIndex = j
            if clusterAssment[i, 0] != minIndex: # 和之前所属类不同，继续循环
                clusterChanged = True
            clusterAssment[i, :] = minIndex, minDist ** 2   # 将minindex，mindist分别给clusterassment的第一列和第二列
            print(centroids)
        for cent in range(k):   #重新计算聚类中心，cent从0遍历到k
            ptsInClust = dataSet[nonzero(clusterAssment[:, 0].A == cent)[0]]
            # 加上判断
            if len(ptsInClust) != 0:# 在选出其他分类所对应的数据集时，由于会产生空的数组，传入mean()函数中 不为空时再传入
                centroids[cent, :] = mean(ptsInClust, 0)
        """  #clusterAssment[:,0]:取得clusterAssment中第0列元素。
                                       #clusterAssment[:,0].A：转置成一个1行m列的行矩阵
                                       #clusterAssment[:,0].A==cent ：将行矩阵中每一个元素与
                                       cent进行比较，得到一个1行m列、元素取值为True和false
                                       的矩阵，元素为true表示该样本是第cent个聚类中心的点
                                       #nonzero(clusterAssment[:,0].A==cent)[0]：获得元素值为
                                       True的元素下标，这些下标集合即为所有属于cent类的样 本下标
                                       #整句含义：取得数据集中属于第cent个簇的样本集
            """
        '''
            # centroids[cent, :] = mean(ptsInClust, axis=0)
           
            mean()计算平均值
            axis = 0：压缩行，对各列求均值，返回 1* n 矩阵
            '''
    return centroids, clusterAssment

# 可视化
def show(dataSet, k, centroids, clusterAssment):
    from matplotlib import pyplot as plt    #导入库函数
    numSamples, dim = dataSet.shape # 返回数据集的行数以及列数，分别赋给numSamples和dim
    mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr'] #样本各种形状颜色
    for i in range(numSamples): #遍历数据集
        markIndex = int(clusterAssment[i, 0])
        plt.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex]) # 标出数据集
    mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', '<b', 'pb'] # 中心的形状样式
    for i in range(k):  # 画出中心点
        plt.plot(centroids[i, 0], centroids[i, 1], mark[i], markersize=10)
    plt.show()


def main():
    # dataMat = mat(loadDataSet('testSet.txt')) # 加载数据集。若没有源数据，可用下面两句随机生成数据
    dataMat = random.rand(100, 2)   #随机生成100行2列的数据
   	dataMat = mat(dataMat)  # 矩阵化
    myCentroids, clustAssing = kMeans(dataMat, 3)       # 调用k-means算法，返回属于那一类，以及距离
    print(myCentroids)
    show(dataMat, 3, myCentroids, clustAssing)  # 可视化


if __name__ == '__main__':
    """ python代码按照顺序从头到尾执行，不执行def开头的函数，def函数只有被调用时才执行。
        本句意思是：判断正在执行的程序是否有主函数，若有，则不执行下面这行语句；若没有，则调用main函数
    """
    main()

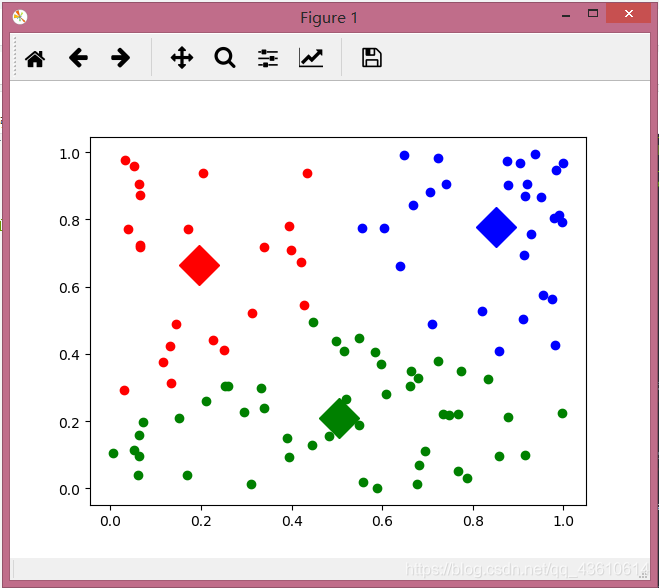
运行结果：