PID控制器的FPGA实现

原创已于 2024-06-19 11:31:18 修改 · 2.2k 阅读

18 ·

CC 4.0 BY-SA版权

文章标签：

#fpga开发

于 2024-06-19 11:28:57 首次发布

首先，PID控制（Proportional-Integral-Derivative Control）是一种广泛应用于工业控制系统中的反馈控制算法。其核心思想是通过对控制误差的比例、积分和微分进行计算和组合，以实现对系统的精确控制。

我们分开来看PID控制的P控制，I控制和D控制。

首先需要知道几个变量的物理意义：

SV：Set Value 设定的目标值；

CV：Current Value 系统当前值；

E(t) = SV — CV；当前误差值；

U(t)：待增加的值（连续）；

U(x)：待增加的值（离散）。

这里先给出连续状态和离散状态下的公式，在连续状态下：

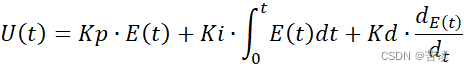
在离散状态下：

上面两个式子中，三个部分分别表示P-I-D控制，Kp，Ki，Kd分别表示调试的系数，接下来看看三个控制方法，以将转速为0的电机调整到100转为例子（设定Kp，Ki，Kd都为0.5）。

（1）P控制（比例控制）：，此处为100。，Kp为0.5。则有输出Y = 0 + 50等于50，将50当做CV的值，下一次引入过后，输出Y则为75，以此类推，很容易就将达到100。当然，这是理想的情况，实际上因为电路的阻抗的消耗和电机老化，不可能达到100，大概只有90，这就和我们想的不一样，会一直存在E(t) = 10。电机实际转速始终只有90，这叫稳态误差；如何来消除稳态误差呢？我们使用积分来估算误差。

（2）I控制（积分控制）：当存在稳态误差的情况下，通过比例控制已经无法消除CV和SV之间的稳态误差了，此时每一个循环都会存在相同的误差E(t)，但我们的目标应当是E(t)逐渐减小的，因为稳态误差的存在，会一直有一个E(t)，这里引入积分控制就可以消除该稳态误差，为什么呢？之前学过的高等数学知识有讲到，积分的物理意义是一段时间内，物理量的总和。如果对之间的所有误差值E(t)进行积分，就可以表示前面所有的E(t)的和，当进入稳态误差的状态后，虽然E(t)保持不变，但此时，是不断累积的，因此，U(t)的值就会增大，从而导致输出增大，以使CV = U(t)+CV不断逼近SV的值。那么问题来了，引入积分控制之后，在进入稳态误差状态之前又会有什么样的现象呢？在前两次循环的时候，因为的累计，会导致U(t)的值很大，使得CV = U(t)+CV超过SV的值，此时的E(t) = SV – CV，E(t) < 0,又会使得的值降低，从而使CV朝着SV逼近，如下图所示：

观察上图，在进入一个较稳定的状态之前，会有一段震荡，高于目标值SV的震荡是我们不愿意看到的，因为我们的系统的最大值如果是100，目标值设置为100，上面的部分就是超出系统的性能范畴，可能引起设备故障，我们把该现象叫做超调。

（3）D控制，即微分控制，在公式上是，当误差E(t)快速变化时，也会变大，从而使U(t)的值快速调整，以抵消误差的变化，在无人机姿态控制中，姿态误差的快速变化会导致微分项增加，控制器快速调整电机转速，抵消姿态的急剧变化，保持机身稳定。

综上所述，理想状态下（无摩擦，无设备损坏，无电路阻抗等）比例控制可以很好的进行设备控制，但理想情况下是不存在的，积分控制可以很好的抵消各种因素导致的误差，这就是PID控制算法的厉害之处了，而积分的引入会导致，系统震荡和超调，使用微分控制可以稳定系统震荡。

在介绍完上述控制算法的基础知识过后，我们来想想如何利用FPGA实现该算法呢？根据上述公式和理解不难发现，该系统存在反馈，反馈的值需要不断的进入系统后进行循环运算。因此，使用状态机可以很好的实现该公式，装填图设计如下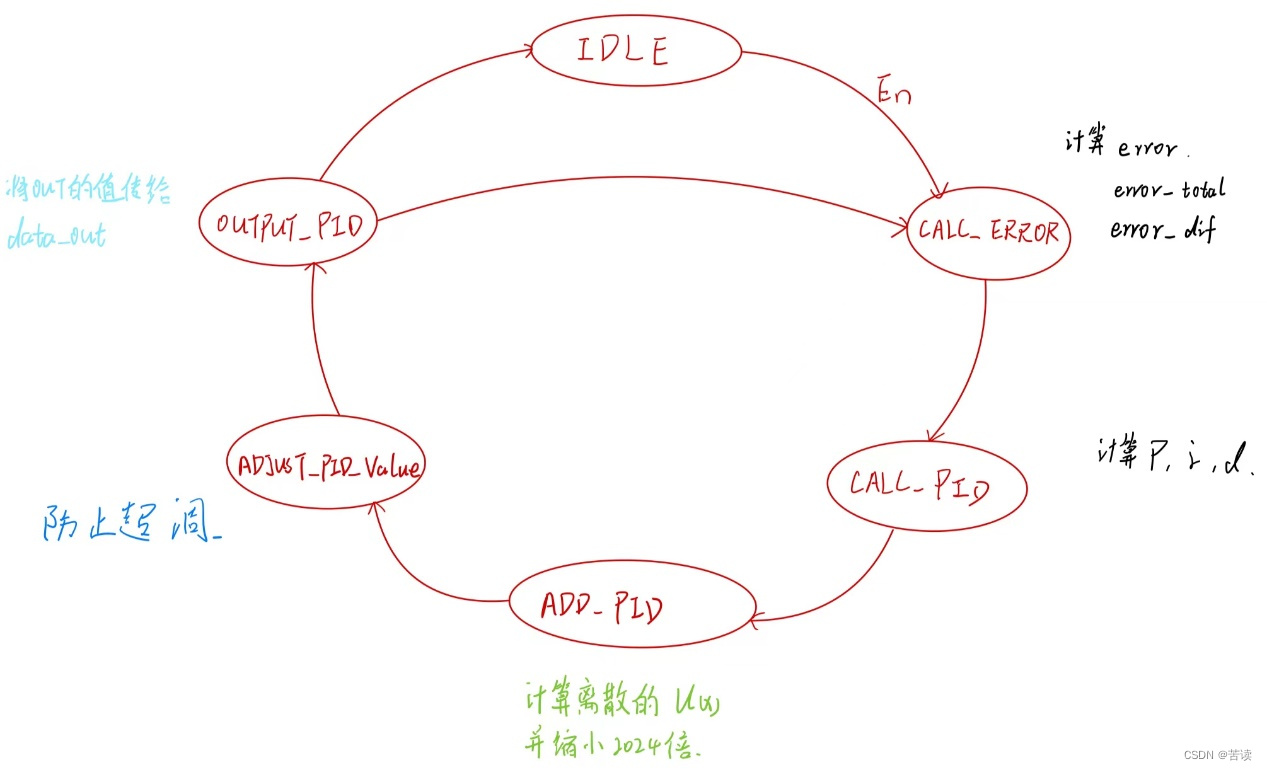：根据状态图写出的状态转移代码如下图所示：

case (state)
            IDLE:              next_state = pid_start ? CALC_ERROR : IDLE;
            CALC_ERROR:        next_state = CALC_PID;
            CALC_PID:          next_state = ADD_PID;
            ADD_PID:           next_state = ADJUST_PID_VALUE;
            ADJUST_PID_VALUE:  next_state = OUTPUT_PID;
            OUTPUT_PID:        next_state = FEED_BACK;
            FEED_BACK:         next_state = (!pid_start) ? IDLE : CALC_ERROR;
endcase

仿真结果如下图所示：