二维数组经典问题

解决二维数组问题需要注意的几个点：

• 二维数组中行数和列数不一定相同，注意具体情况
• 多通过画图等手段找到索引之间的规律
• 注意数组的边界条件

旋转矩阵

旋转90度实际上是四个数字交换位置，那么我们只要遍历四分之一的数组，每次找到另外三个点，交换它们的位置就可以了。

如何交换呢，我们假设4个数字按顺时针顺序分别为1,2,3,4，则交换以后原来位置上应该是4,1,2,3.

而需要遍历的那四分之一数组就是正方形的上边为底的等腰直角三角形，如下图，注意三角的右对角线上的数字是不用遍历的，因为它们与左对角线重复了。

public class Solution {
    public void Rotate(int[][] matrix) {
        int size=matrix.Length;
        int i,j;
        for(i=0;i<size/2;i++)
        for(j=i;j<size-i-1;j++)
        r(matrix,i,j,size);

    }
    public void r(int[][] matrix,int i,int j,int size)
    {
        int a,b,c,d;
        a=matrix[i][j];
        b=matrix[j][size-1-i];
        c=matrix[size-1-i][size-1-j];
        d=matrix[size-1-j][i];
        matrix[i][j]=d;
        matrix[j][size-1-i]=a;
        matrix[size-1-i][size-1-j]=b;
        matrix[size-1-j][i]=c;
    }
}

 零矩阵

编写一种算法，若M × N矩阵中某个元素为0，则将其所在的行与列清零。

注意这题中矩阵的行数和列数可能是不同的。

我们先遍历矩阵，用一个数组记下所有为零的索引，再根据索引矩阵将同行和列的都变为零。

public class Solution {
    public void SetZeroes(int[][] matrix) {
        int sizex=matrix.Length;
        int sizey=matrix[0].Length;
        int[,] index=new int[sizex*sizey,2];
        int i,j,k=0;
        for(i=0;i<sizex;i++)
        for(j=0;j<sizey;j++)
        {
            if(matrix[i][j]==0)
            {
                index[k,0]=i;
                index[k,1]=j;
                k++;
            }
        }
        if(k!=0)
        for(i=0;i<k;i++)
        {
            int x=index[i,0];
            int y=index[i,1];
            for(j=0;j<sizey;j++)
            matrix[x][j]=0;
            for(j=0;j<sizex;j++)
            matrix[j][y]=0;
        }
    }
}

 对角线遍历

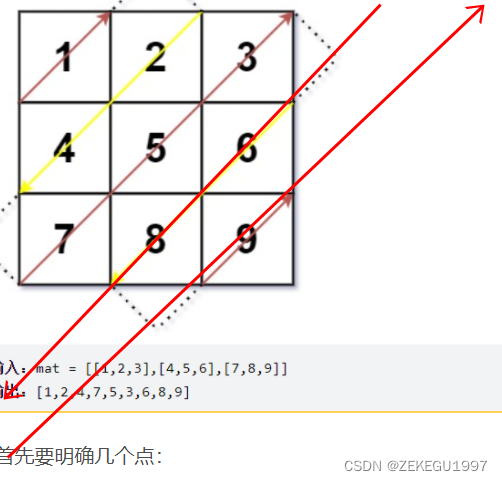
 这题首先要明确几个点：

• 对角线的条数=m+n-1
• 每条对角线上的索引之和相同
• 第i条对角线的方向是根据i的奇偶性决定的
• 当对角超过矩阵的对角线时，它的开始和结束条件是比较复杂的

针对第四点，我们不妨把矩形的左边和上边延长，使得对角线可以从行标或列表为开始，然后再把不符合边界条件的剔除。如下图所示

 

public class Solution {
    public int[] FindDiagonalOrder(int[][] mat) {
        int m=mat.Length;
        int n=mat[0].Length;
        int i,j,k=0;
        int[] a=new int[m*n];
        for(i=0;i<m+n-1;i++)
        {
            for(j=0;j<=i;j++)
            {
                if(i%2==1&&j<m&&i-j<n)
                {a[k]=mat[j][i-j];k++;}
                if(i%2==0&&i-j<m&&j<n)
                {a[k]=mat[i-j][j];k++;}
            }
        }
        return a;
    }
}