牛客练习赛53——B.美味果冻

前言
又是一个只过了签到题的比赛，蒟蒻又来补题了。

题目链接

https://ac.nowcoder.com/acm/contest/1114/B

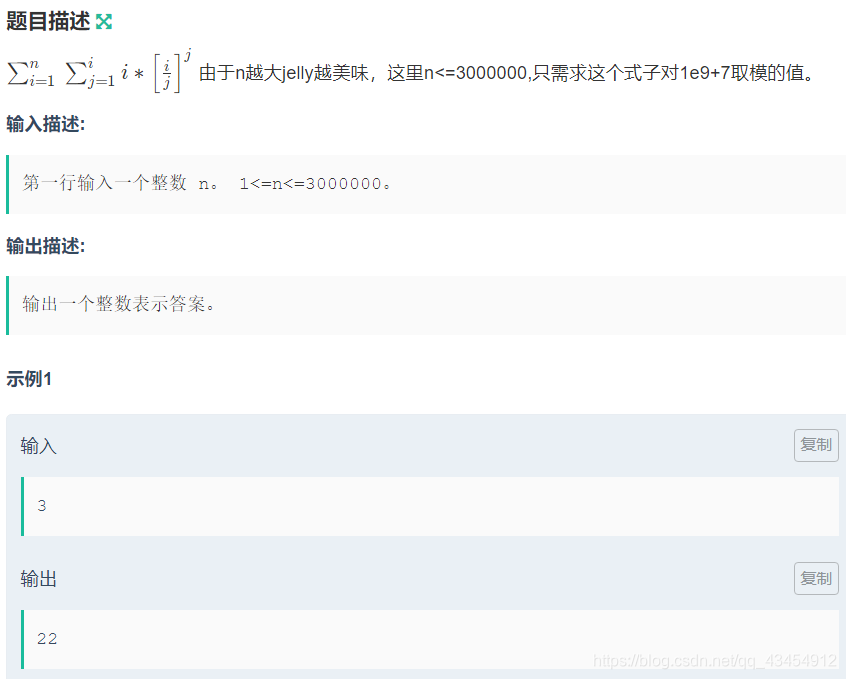
题目理解

蒟蒻看到这一题就想用暴力做，无奈n很大，暴力只会超时。做的时候想过将${\sum }_{i=1}^n$${\sum }_{j=1}^i$变换一下，但是蒟蒻太菜了，于是愉快的等到比赛结束去看题解。题解里果然是交换成${\sum }_{j=1}^n$${\sum }_{i=j}^n$，为什么可以这样交换可以看下面的图。把两个式子看成同一个下三角矩阵就行了，两个是一摸一样的。

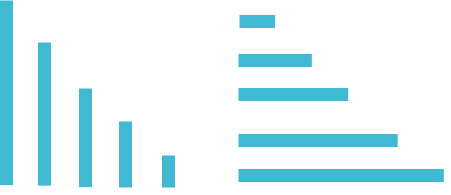
• 对原式${\sum }_{i=1}^n{\sum }_{j=1}^{i}i\ast (\lceil \frac{i}{j}\rceil {)}^j$来说， j在内循环而且它还是指数，很不好写程序，要考虑的东西很多。但是交换一下顺序就不同了。
• 换成${\sum }_{j=1}^n{\sum }_{i=j}^{n}i\ast (\lceil \frac{i}{j}\rceil {)}^j$后，j在外层，那么对于内循环来说只需要考虑i作为变量，把i与$(\lceil \frac{i}{j}\rceil {)}^j$分开计算即可。
• 考虑n很大，可以采用更快速的方法，这里我们找$(\lceil \frac{i}{j}\rceil {)}^j$的规律。

打表如下

可以看出$(\lceil \frac{i}{j}\rceil {)}^j$可以把n分成$\frac{n}{j}$块，然后每一块的分别算幂，用快速幂也会超时，所以需要用数组模拟每一块的幂。对于计算i可以用每一块长度的等差求和公式来计算。但是对于长度不满$\frac{n}{j}$的块来说，需要处理一下单独的长度就行了。

AC代码

//思维+分块+模拟快速幂+取模+数列公式 
#include<iostream>
#define int long long
using namespace std;
const int maxn = 3e7 +10;
const int mod = 1e9+7;
signed main(){
	int n;
	scanf("%lld",&n);
	int prime[maxn];
	fill(prime,prime+n+1,1);
	int ans=0;
	for(int j=1;j<=n;j++){
		int k=n/j;
		int l=j;
		int r=j+j-1;
		for(int i=1;i<k;i++){
			prime[i]=1LL*prime[i]*i%mod;   
			ans=(ans+(1LL*((r+l)*j/2%mod)*prime[i]%mod))%mod;
			l+=j;
			r+=j;
		}
		prime[k]=1LL*prime[k]*k%mod;
		ans=(ans+1LL*(l+n)*(n-l+1)/2%mod*prime[k]%mod)%mod;
	}
	printf("%lld",ans);
	return 0;
}