先给出结论,Vivado中的加法器是利用SLICE中的LUT和进位链实现的。
一、全加器
一位全加器的结构如下:

其中:
- A、B为输入的两个加数
- CI为进位
- CO为本位对高位的进位
- S为本位和
输出与输入的逻辑关系为:
S = A ⊕ B ⊕ C i n C o u t = A B + B C i n + A C i n S=A\oplus B\oplus C_{in}\\ C_{out}= AB+BC_{in}+AC_{in} S=A⊕B⊕CinCout=AB+BCin+ACin
二、SLICE如何实现加法器
SLICEM的结构如下:

CARRY4进位链结构如下:

介绍图中几个信号的含义:
- CIN:进位信号
- DI:数据输入,两个加数或的结果;
- O:本位和
- CO:本位对高位的进位
- S:两个加数异或的结果
参考全加器输出与输入的对应关系
S = A ⊕ B ⊕ C i n C o u t = A B + B C i n + A C i n S=A\oplus B\oplus C_{in}\\ C_{out}= AB+BC_{in}+AC_{in} S=A⊕B⊕CinCout=AB+BCin+ACin
再观察下图中红色框部分,其中,LUT的O6输出(O6 From LUTA)和进位CIN进行异或得到输出AMUX,对比公式可知这个为本位和的输出,,可以选择直接输出也可以选择经过触发器同步输出。

而本位对高位的进位在图中是如何体现的呢?
首先明确四个信号,在图中已标出:

当S0为0时,MUX输出左边的DI,若S0为1则输出CIN。
具体分析如下:
-
若S0为0说明两个加数要么为00,要么为11,此时输出的是DI即两个加数相或的结果
①如果为0表明两个加数为00,DI为0,根本不会产生进位,因此CO0输出0;
②如果为1表明两个加数为11,DI为1,一定会产生进位,因此CO0输出1;
两种情况下CO0的输出和DI的值相同。
-
若S0为1表明两个加数中只有一个1,这时只要CIN为1就有进位,CO0输出1;为0 则没有进位,CO0输出0,CO0的输出与CIN值相同。
那重点是如何实现让S表示两个数异或的结果,让DI表示两数相互或的结果?
这就利用到将1一个六输入LUT当作两个5输入LUT的原理。LUT6的结构如下:
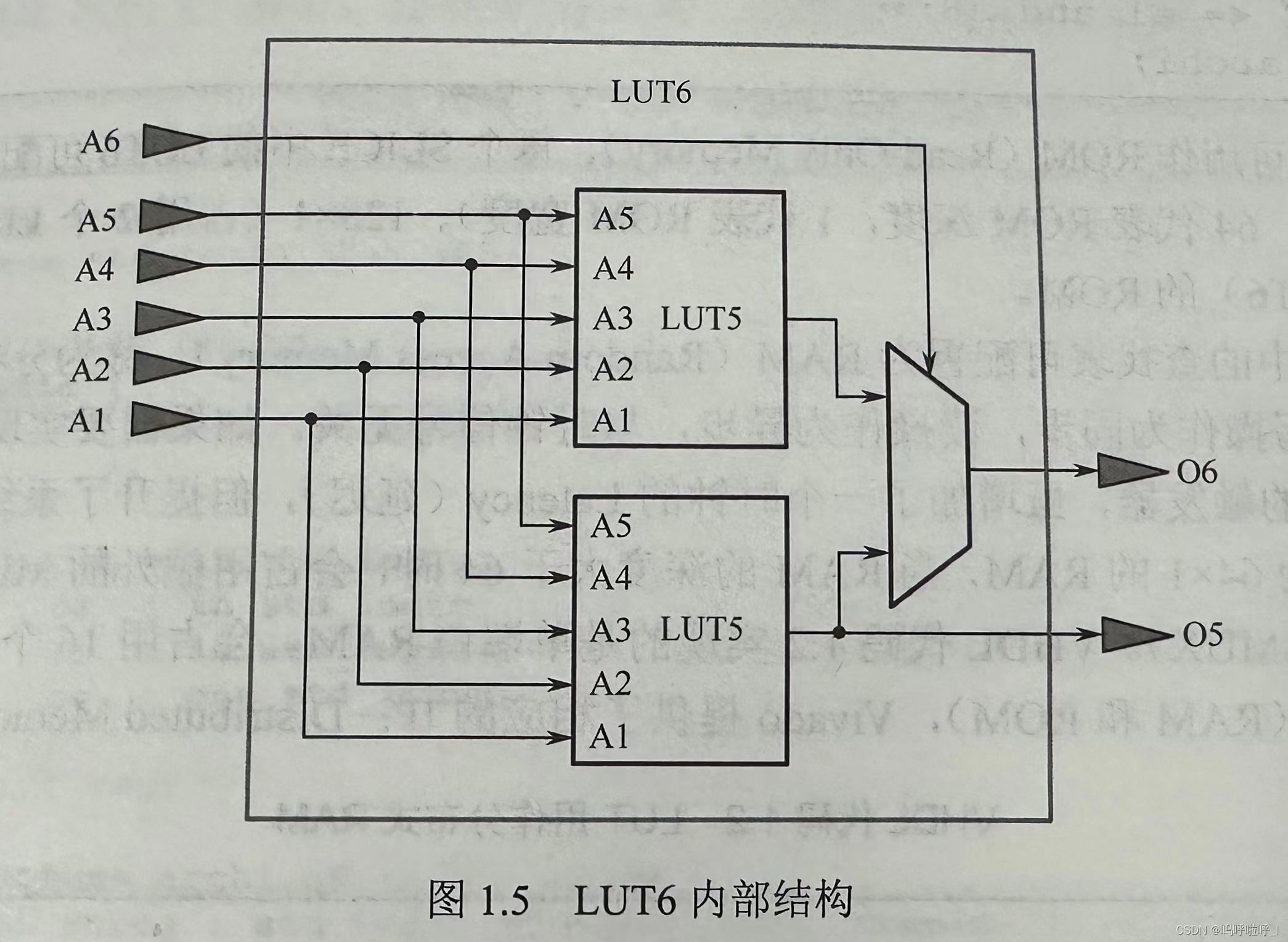
因此我们需要将上面LUT5的输出对应S,下面的LUT5输出对应DI,如何实现?就是通过填写LUT5的初始值(LUT就像真值表一样,根据输入的情况产生对应的输出)。
三、实例测试
1.直接使用加法器
module full_add(
input [7:0] a,
input [7:0] b,
input c_in,
output [7:0] sum
);
assign sum=a+b+c_in;
endmodule
综合后的电路为:

大部分电路结构和我们上述分析的是一致的,但是我们也会发现有几个不同的地方(仅分析低4bit对应的电路):
(1)b[0]没有和a[0]连入一个查找表,而是b[0]连接到动态进位输入CYINIT,a[0]和c_in构成了查找表的输出S0;
(2)DI连接的不少查找表的O5输出,而是连接的a[3:0]
S = a ⊕ c i n D I = a S=a\oplus c_{in} \\DI=a \\ S=a⊕cinDI=a
而原来的情况下:
S = a ⊕ b D I = a + b S=a\oplus b \\DI=a+b \\ S=a⊕bDI=a+b
那这样的效果和之前描述的效果一样吗?
首先可以明确的是对于本位和是没有影响的,因为本位和是三者的异或。将b[0]和c_in换位置并不影响。
但是本位对高位的进位就不一定了,因为要经过S控制的MUX,做如下分析:
之前说过S为0选择DI输出,S为1选择低位对本位的进位(对于第一级就是b)输出。
①假设c_in为0
| a | b | S | DI | C[0] |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
符合要求。
②假设c_in为1
| a | b | S | DI | C[0] |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
也符合要求。
但是不理解为什么会综合成这个结果…
2.LUT级别
为能够更深入的理解进位链的结构和LUT的关系,给出采用LUT级别实现加法器的例子。
参考LUT6的结构发现其为两个LUT5的组合,因此给出两个5输入LUT真值表如下:
(1)上面LUT5的真值表(两个输入异或,用于输出O6)
| I4-I2 | I0(a) | I1(b) | O6 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
(2)下面LUT5的真值表(两个输入相或,用于输出O5)
| I4-I2 | I0(a) | I1(b) | O6 |
|---|---|---|---|
| x | 0 | 0 | 0 |
| x | 0 | 1 | 1 |
| x | 1 | 0 | 1 |
| x | 1 | 1 | 1 |
module ADD_lut(
input rst,
input clk,
input CE,
input [7:0]a,
input [7:0]b,
output [7:0]sum,
output [7:0]co
);
wire [7:0]sum;
wire [7:0]lut_o6;
wire [7:0]lut_o5;
LUT6_2#(.INIT(64'h66666666EEEEEEEE))LUT6_2_inst0(.O6(lut_o6[0]),.O5(lut_o5[0]),.I0(a[0]),.I1(b[0]),.I2(0),.I3(0),.I4(0),.I5(1));
LUT6_2#(.INIT(64'h66666666EEEEEEEE))LUT6_2_inst1(.O6(lut_o6[1]),.O5(lut_o5[1]),.I0(a[1]),.I1(b[1]),.I2(0),.I3(0),.I4(0),.I5(1));
LUT6_2#(.INIT(64'h66666666EEEEEEEE))LUT6_2_inst2(.O6(lut_o6[2]),.O5(lut_o5[2]),.I0(a[2]),.I1(b[2]),.I2(0),.I3(0),.I4(0),.I5(1));
LUT6_2#(.INIT(64'h66666666EEEEEEEE))LUT6_2_inst3(.O6(lut_o6[3]),.O5(lut_o5[3]),.I0(a[3]),.I1(b[3]),.I2(0),.I3(0),.I4(0),.I5(1));
LUT6_2#(.INIT(64'h66666666EEEEEEEE))LUT6_2_inst4(.O6(lut_o6[4]),.O5(lut_o5[4]),.I0(a[4]),.I1(b[4]),.I2(0),.I3(0),.I4(0),.I5(1));
LUT6_2#(.INIT(64'h66666666EEEEEEEE))LUT6_2_inst5(.O6(lut_o6[5]),.O5(lut_o5[5]),.I0(a[5]),.I1(b[5]),.I2(0),.I3(0),.I4(0),.I5(1));
LUT6_2#(.INIT(64'h66666666EEEEEEEE))LUT6_2_inst6(.O6(lut_o6[6]),.O5(lut_o5[6]),.I0(a[6]),.I1(b[6]),.I2(0),.I3(0),.I4(0),.I5(1));
LUT6_2#(.INIT(64'h66666666EEEEEEEE))LUT6_2_inst7(.O6(lut_o6[7]),.O5(lut_o5[7]),.I0(a[7]),.I1(b[7]),.I2(0),.I3(0),.I4(0),.I5(1));
CARRY4 CARRY4_inst0(.CO(co[3:0]),.O(sum[3:0]),.CI(1'b1),.CYINIT(1'b0),.DI(lut_o5[3:0]),.S(lut_o6[3:0]));
CARRY4 CARRY4_inst1(.CO(co[7:4]),.O(sum[7:4]),.CI(co[3]),.CYINIT(1'b0),.DI(lut_o5[7:4]),.S(lut_o6[7:4]));
FDRE FDRE_inst0(.Q(o_sum[0]),.C(clk),.CE(CE),.R(rst),.D(sum[0]));
FDRE FDRE_inst1(.Q(o_sum[1]),.C(clk),.CE(CE),.R(rst),.D(sum[1]));
FDRE FDRE_inst2(.Q(o_sum[2]),.C(clk),.CE(CE),.R(rst),.D(sum[2]));
FDRE FDRE_inst3(.Q(o_sum[3]),.C(clk),.CE(CE),.R(rst),.D(sum[3]));
FDRE FDRE_inst4(.Q(o_sum[4]),.C(clk),.CE(CE),.R(rst),.D(sum[4]));
FDRE FDRE_inst5(.Q(o_sum[5]),.C(clk),.CE(CE),.R(rst),.D(sum[5]));
FDRE FDRE_inst6(.Q(o_sum[6]),.C(clk),.CE(CE),.R(rst),.D(sum[6]));
FDRE FDRE_inst7(.Q(o_sum[7]),.C(clk),.CE(CE),.R(rst),.D(sum[7]));
FDRE FDRE_inst8(.Q(o_sum[8]),.C(clk),.CE(CE),.R(rst),.D(co[7]));
endmodule
综合出来的电路结构如下:

这个就和上述介绍的完全一致了。










 本文详细介绍了Vivado设计工具中利用SLICE中的LUT和进位链实现加法器的过程,包括全加器结构、SLICE工作原理以及实例测试,展示了如何通过LUT级联来构建加法器功能。
本文详细介绍了Vivado设计工具中利用SLICE中的LUT和进位链实现加法器的过程,包括全加器结构、SLICE工作原理以及实例测试,展示了如何通过LUT级联来构建加法器功能。

















 1337
1337

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








