图的遍历——广度优先遍历BFS/BFT

7.3.2 图的深度优先遍历(Breadth First Traversal)

1. 图的广度优先遍历基于广度优先搜索（breadth first search，BFS），广度优先搜索是从图中某一顶点v出发，在访问顶点v后再访问v的各个未曾被访问过的邻接顶点w1，w2，…，wk，然后再依次访问w1，w2，.…，wk 的所有还未被访问过的邻接顶点。再从这些访问过的顶点出发，再访问它们的所有还未被访问过的邻接顶点……如此下去，直到图中所有和顶点v由路径连通的顶点都被访问到为止。
   广度优先搜索是一种分层的搜索过程，它类似于树的层次遍历。
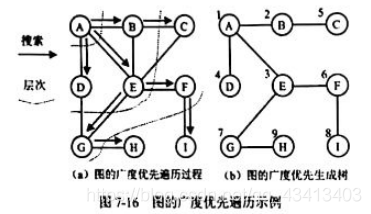
2. 图7-16（a）给出了一个从顶点A出发进行广度优先遍历的示例。
   
   图7-16（b）给出了由广度优先遍历得到的广度优先生成树，它由遍历时访问过的n个顶点和遍历时经历的n-l条边组成，各顶点旁边的数字标明了顶点被访问的顺序。
   从图7-16（a）中可以看出，搜索每向前走一步可能访问一批顶点，不像深度优先搜索那样有往回退的情况，因此，广度优先遍历不是一个递归的过程，其算法也不是递归的。为了实现逐层访问，算法中使用了一个队列，以记录刚才访问过的上一层和本层顶点，以便于向下一层访问。
3. 从指定的结点v开始进行广度优先搜索的算法思想：
   1）访问结点v，并标记v已枝访问，同时顶点v入队列。
   2）当队列空时算法结束，否则继续步骤(3)。
   3）队头顶点出队列为v。
   4）取顶点v的第一个邻接顶点w。
   5）若顶点w不存在，转步骤(3)：否则继续步骤(6)。
   6）若顶点w未被访问，则访问结点w.并标记w已被访问，同时顶点w入队列；否则继续步骤(7)。
   7）使w为顶点v的在原来w之后的下一个邻接顶点，转到步骤(5)。
4. 广度优先遍历 BFT 代码实现
   利用无向图邻接矩阵。

#include "AdjMatrixUndirGraph.h"		// 无向图邻接矩阵
#include <queue>

///广度优先搜索 BFS
template <class ElemType>
void BFS(const AdjMatrixUndirGraph<ElemType> &g, int v, void (*Visit)(const ElemType &))
// 初始条件：存在图g
// 操作结果：从顶点v出发进行广度优先搜索
{
   
   
    queue<int> q;
    int u, w;
    ElemType e;
    g.SetTag(v, VISITED);						// 作访问标志
    g.GetElem(v, e);							// 取顶点v的数据元素值
    Visit