有源滤波器

最新推荐文章于 2025-04-03 21:47:05 发布

Only and one.

最新推荐文章于 2025-04-03 21:47:05 发布

阅读量2.5k

点赞数 20

文章标签：信号处理

本文链接：https://blog.youkuaiyun.com/qq_43411800/article/details/136202683

版权

本文介绍了有源滤波器的概念，重点讲解了RC低通和高通滤波器的设计，包括电容元件的工作原理、电流与电压的关系以及截止角频率和传递函数的计算。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

信号处理：滤波、采样、比较。

有源滤波器

滤波器：即选频电路，有低通、高通、带通及带阻等。

有源滤波器：运算放大器是有源器件，所以带有放大器的滤波电路称为有源滤波器。与无源滤波器比较，有源滤波器具有体积小、效率高、频率特性好等一系列优点。

在进行有源滤波器的介绍之前，让我们了解一些有源滤波器设计的元器件，比如电容、电阻等，电阻都是我们常见常用的元器件，在此不再赘述。

图1 RC低通滤波电路

电容元件

如图1所示，为RC低通滤波电路，我们对此电路做进一步详细的分析。

电容，即容纳电荷的能力，其参数

$C=\frac{q}{u}$ (1-1)

当电容元件上电荷[量]发生变化时，则在电路中引起电流

$i=\frac{dq}{dt}=C\frac{du}{dt}$ (1-2)

当电容两端加恒定电压时，其中电流 $i$ 为零，电容元件可视为开路，即通交隔直。

$\int_{0}^{t}uidt=\int_{0}^{t}Cudu=\frac{1}{2}Cu^{2}$ (1-3)

表明电容元件是为储能元件。

电容元件的交流电路

由式(1-2)，如果在电容器件的两端加一正弦电压 $u=U_{m}sin(wt)$ ，则

$i=C\frac{U_{msin(wt)}}{dt}=wCU_{m}sin(wt+90^{\circ})=I_{m}sin(wt+90^{\circ})$ (1-4)

由式(1-4)可知，在电容元件电路中，在相位上电流比电压超前90°。（规定：电流比电压滞后时，其相位差为正；当电流比电压超前时，其相位差为负，这样的规定是为了说明电路是电感性的还是电容性的）

由式(1-4)可得，

$I_{m}=wCU_{m}$ (1-5)

有源低通滤波器

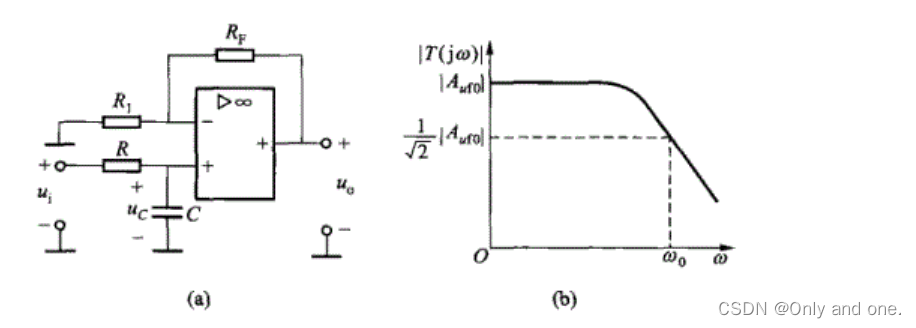
图2 有源低通滤波器

图2所示，为有源低通滤波器电路示意图，设输入电压 $u_1$ 为某一频率的正弦电压，则可用相量表示。由RC电路及式(1-5)，可得

$\dot{U_+}=\dot{U_c}=\frac{\frac{1}{jwC}}{R+\frac{1}{jwC}}\cdot\dot{U_i}=\frac{\dot{U_i}}{1+jwRC}$ (1-6)

根据同相比例运算，可得

$\dot{U_0}=(1+\frac{R_F}{R_1})\dot{U_+}$ (1-7)

$\therefore$

$\frac{\dot{U_0}}{\dot{U_i}}=\frac{1+\frac{R_F}{R_1}}{1+jwRC}=\frac{1+\frac{R_F}{R_1}}{1+j\frac{w}{w_0}}$ (1-8)

式中， $w_0=\frac{1}{RC}$ 称为截止角频率

传递函数

$T_{jw}=\frac{\dot{U_0}}{\dot{U_i}}=\frac{1+\frac{R_F}{R_1}}{1+j\frac{w}{w_0}}= \frac{A_{uf0}}{1+j\frac{w}{w_0}}$ (1-9)

不难得出

$\left \| T(jw) \right \|=\frac{\left \| A_{uf0} \right \|}{\sqrt{1+(\frac{w}{w_0})^2}}$ $\varphi(jw)=-arctan(\frac{w}{w_0})$
角频率 $w$	传递函数 $\left \| T(jw) \right \|$	备注
0	$\left \| A_{uf0} \right \|$
$w_0$	$\frac{\left\| A_{uf0}\right\|}{\sqrt{2}}$
$\infty$	0

有源高通滤波器

图3 有源高通滤波器

由RC电路可得

$\dot{U_+}=\dot{U_c}=\frac{R}{R+\frac{1}{jwC}}\cdot\dot{U_i}=\frac{\dot{U_i}}{1+\frac{1}{jwRC}}$ (1-10)

根据同相比例运算电路可得

$\frac{\dot{U_0}}{\dot{U_i}}=\frac{1+\frac{R_F}{R_1}}{1+1+\frac{1}{jwRC}}=\frac{1+\frac{R_F}{R_1}}{1-j\frac{w_0}{w}}$ (1-11)

式中， $w_0=\frac{1}{RC}$ 。

传递函数

$T_{jw}=\frac{\dot{U_0}}{\dot{U_i}}=\frac{1+\frac{R_F}{R_1}}{1-j\frac{w_0}{w}}= \frac{A_{uf0}}{1-j\frac{w_0}{w}}$ (1-12)

不难得出

$\left \| T(jw) \right \|=\frac{\left \| A_{uf0} \right \|}{\sqrt{1+(\frac{w_0}{w})^2}}$ $\varphi(jw)=arctan(\frac{w_0}{w})$
角频率 $w$	传递函数 $\left \| T(jw) \right \|$	备注
0	0
$w_0$	$\frac{\left\| A_{uf0}\right\|}{\sqrt{2}}$
$\infty$	$\left \| A_{uf0} \right \|$