最优化方法——一维搜索算法之黄金分割法及其Matlab实现

最新推荐文章于 2023-09-19 22:32:46 发布

原创

最新推荐文章于 2023-09-19 22:32:46 发布 · 7.5k 阅读

62 ·

CC 4.0 BY-SA版权

黄金分割法是一种用于求解单峰函数极小值的算法，基于区间收缩原理，遵循对称取点、等比收缩和单点计算原则。在Matlab中实现该算法，通过迭代寻找函数最小值。当区间长度小于预设阈值时，返回区间中点作为极小值。在给定初始区间[0, 1]和目标区间长度L≤0.2的情况下，黄金分割法能够有效找到目标函数的最小值。" 89155752,8250317,优化React Native动画性能：保持60 FPS,"['前端开发', 'React', '移动开发', '动画优化', 'React Native']

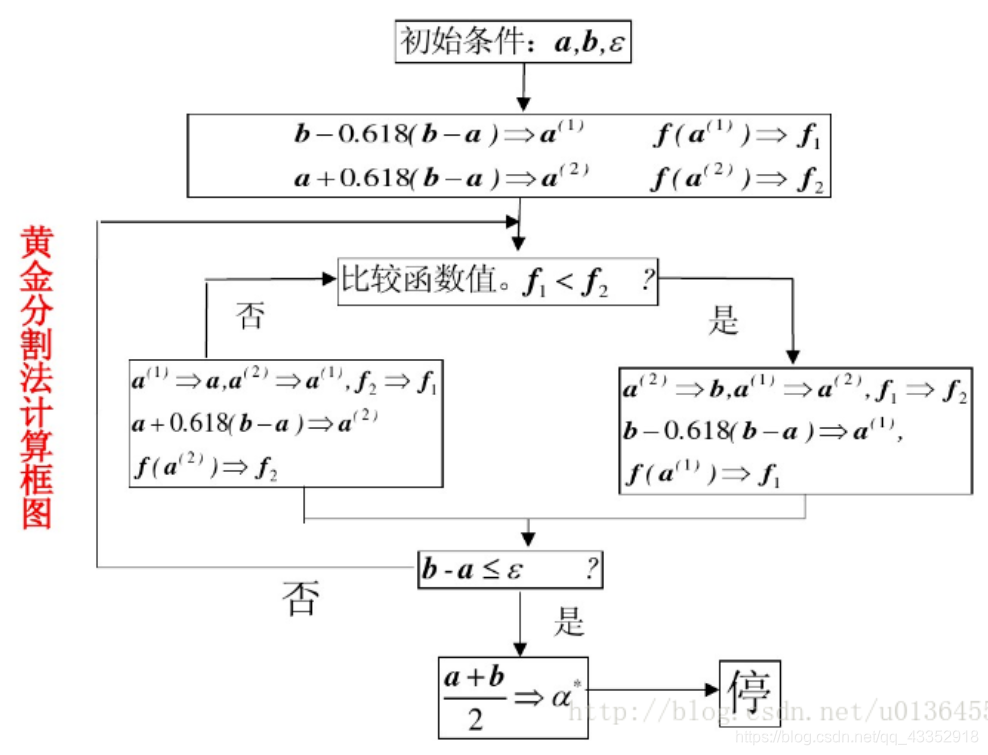
黄金分割法：一种基于区间收缩的求解单峰函数极小值的算法。
三个原则（1）对称取点原则：选取x1，x2使得x₁-a=b-x₂.
（2）等比收缩原则：每次迭代时，让被删除的部分与原来区间的比值保持一个定值。
（3）单点计算原则：每次迭代都只计算一次函数值。
step1：给定a<b,ε>0.
step2：计算x₁:=a+0.382(b-a),x₂:=a+b-x₁.
step3：计算f₁:=f(x₁),f₂:=f(x₂).
step4：如果f₁>f₂,则令a:=x₁,若b-a<ε,则转step5；否则令f₁:=f₂,x₁:=x₂,x₂:=a+0.618(b-a),f₂:=f(x₂),转step4.
否则令b:=x₂,若b-a<ε,则转step5；否则令f₂:=f₁,x₂:=x₁,x₁:=a+0.382(b-a),f₁:=f(x₁),转step4.
step5:停止，输出x*=(a+b)/2.
在这里插入图片描述
黄金分割法Matlab实现代码：