强化学习：策略梯度、Actor-Critic算法

策略梯度、Actor-Critic算法

策略梯度方法

将策略𝜋参数化为𝜋𝜃⁡(𝑎|𝑠)

使得策略变成一个处处可微的概率分布

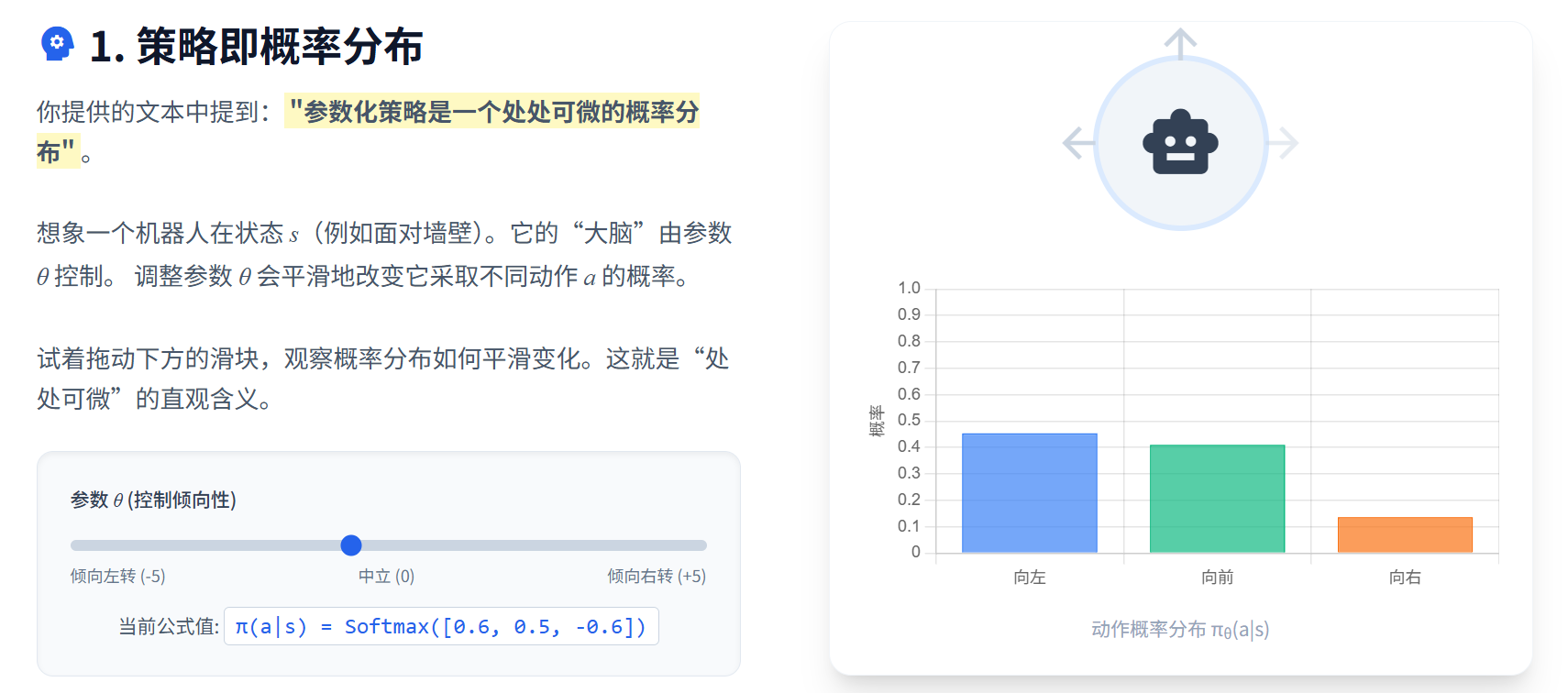
只要能定义出目标函数𝐽⁡(𝜋𝜃)并求出其梯度∇𝜃𝐽⁡(𝜋𝜃)，就能利用梯度下降法来更新参数𝜃，从而使得策略𝜋𝜃逐步逼近最优策略𝜋∗。

最大化长期回报

1、基于轨迹概率密度方式

2、基于平稳分布或状态分布方式，占用测度推导

基于轨迹推导

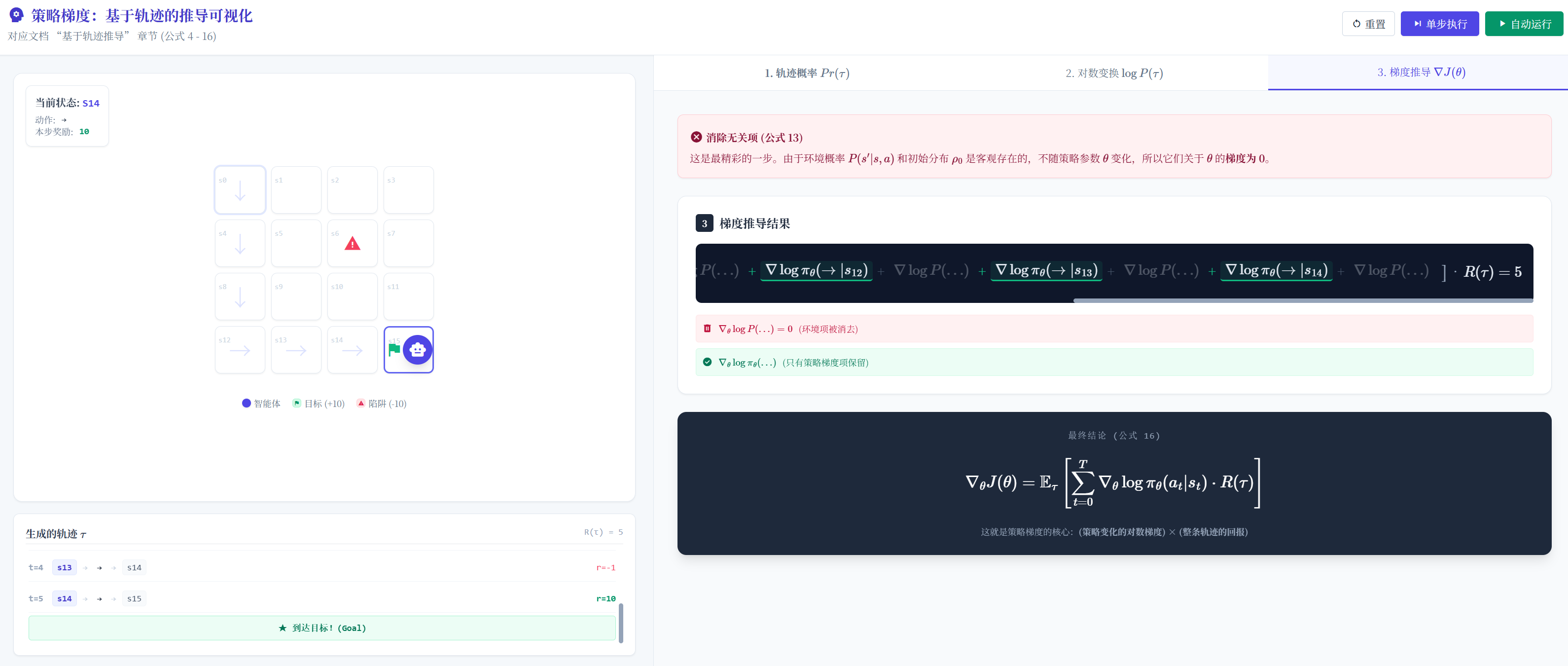
完整的有限步数的交互过程，称为一个 回合（ episode ），回合最大步数用 𝑇 表示 (也叫作 Horizon ②)。把所有状态、动作和奖励组合起来的一个序列，称为 轨迹（ trajectory ），如式 所示。

τ={s0,a0,r0,s1,a1,r1,⋯ ,sT,aT,rT} \tau=\left\{s_{0},a_{0},r_{0},s_{1},a_{1},r_{1},\cdots,s_{T},a_{T},r_{T}\right\} τ={s0​,a0​,r0​,s1​,a1​,r1​,⋯,sT​,aT​,rT​}

轨迹的概率计算过程，状态→状态对应概率→依据策略采样出动作→状态转移概率到下一个状态→状态对应概率

完整轨迹公式

$$\underset{\pi }{\mathrm{Pr}}(\tau )={\rho }_0(s_0)\prod _{t=0}^{T-1}{\pi }_{\theta }(a_t|s_t)P(s_{t+1}|s_t,a_t)$$

可以看出，轨迹概率确实可以写成关于策略𝜋𝜃⁡(𝑎|𝑠)或者策略参数𝜃的函数，如式所示。

$$\underset{\pi }{\mathrm{Pr}}(\tau )=p_{\theta }(\tau )$$

给定策略可能产生很多种轨迹，上面的概率密度变成全概率公式

记每条的轨迹对应的回报为𝑅⁡(𝜏)，根据全概率公式可知，目标函数𝐽⁡(𝜋𝜃)可以表示为轨迹概率密度与对应回报的乘积在所有轨迹上的积分，如式所示。

$$J({\pi }_{\theta })={\int }_{\tau }{p}_{\theta }(\tau )R(\tau )d\tau ={\mathbb{E}}_{\tau \sim p_{\theta }(\tau )}[R(\tau )]$$

占用测度推导

回顾状态价值相关部分，设环境初始状态为𝑠0，那么目标函数𝐽⁡(𝜋)可以表示为初始状态分布𝜌0与对应状态价值𝑉𝜋⁡(𝑠0)的乘积在所有初始状态上的积分，如式所示。

$$J(\pi )={\int }_{s_0}{\rho }_0(s_0)V^{\pi }(s_0)d{s}_0={\mathbb{E}}_{s_0\sim {\rho }_0}[V^{\pi }(s_0)]$$

最终可推导为

$$J({\pi }_{\theta })={\int }_{s_0}{\rho }_0(s_0)\sum _a{\pi }_{\theta }(a|s_0)Q^{{\pi }_{\theta }}(s_0,a)d{s}_0$$

实际上初始状态分布𝜌0会影响智能体后续的状态访问分布（statevisitationdistribution），进而影响目标函数𝐽⁡(𝜋𝜃)的值。

因此，在计算梯度 ∇𝜃𝐽⁡(𝜋𝜃) 时，不能简单地将初始状态分布 𝜌0 视为常数项。为此，需要引入 平稳分布（ stationarydistribution ） 的概念来更好地理解状态访问分布与策略参数 𝜃 之间的关系。

平稳分布

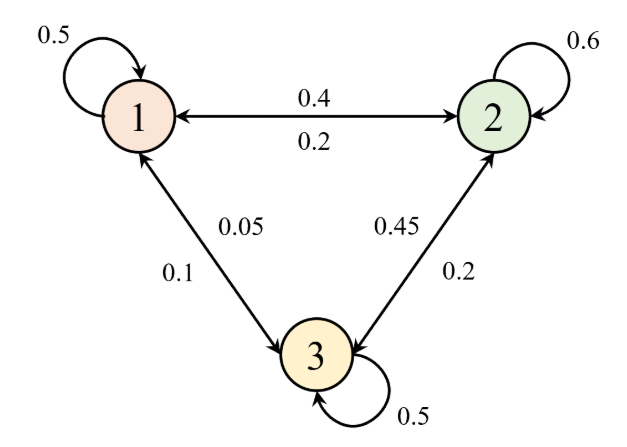
简单来说，它描述了系统在长期运行后，处于各状态的概率分布。需要注意的是，平稳分布的存在是有前提条件的，必须是遍历（ergodic）的马尔可夫过程，遍历包含两个性质：不可约（irreducible）和非周期（aperiodic）。不可约表示从任意状态出发，都有可能到达其他任意状态，有时也叫作连通性（communicative）；非周期表示系统不会陷入某种固定的循环模式。而通常情况下，强化学习中的马尔可夫过程都是遍历的，因此平稳分布是存在的。

策略梯度的通用表达式

$$g=\mathbb{E}\left[\sum _{t=0}^{\infty }{\Psi }_t{\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)\right]$$

Actor-Critic算法

算法类别​	代表算法​	主要优点/成效​	主要缺点/局限性​	核心改进思路​
基于价值 (Value-Based) ​	DQN 系列	在很多任务中取得了不错的效果。	1\. 只能处理**确定性策略**。 2\. 难以适配**连续动作空间**。 3\. 在某些复杂任务中表现不佳。	N/A
纯策略梯度 (Pure Policy Gradient) ​	REINFORCE	在一定程度上解决了确定性策略和连续动作空间的问题。	1\. 存在**高方差**。 2.**采样效率低**。 3\. 难以在复杂环境中取得良好效果。	直接对策略函数进行参数化。
Actor-Critic​	Actor-Critic	**兼顾了前两者的优点**（既解决了动作空间问题，又试图缓解方差和效率问题）。		**结合策略梯度和值函数**： 不仅将策略函数参数化，同时也将值函数参数化。

为了兼顾策略梯度算法的灵活性和基于价值算法的高效性，Actor-Critic算法应运而生，即将值估计的这部分工作交给一个独立的网络（Critic），而策略部分（Actor）则专注于策略的优化。这样不仅可以利用值函数来提供更稳定的梯度估计，还能提高采样效率，从而在复杂任务中取得更好的效果。

算法架构

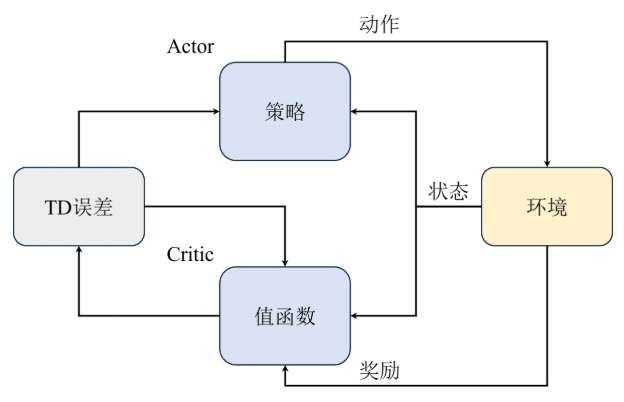
Critic有多种形式：

1、使用状态价值函数$V^{\pi }(s_t)$来估计当前状态的价值

2、使用状态-动作值函数$Q^{\pi }(s_t,a_t)$来估计当前状态-动作对的价值。

使用状态价值函数来表示 Actor-Critic 算法的形式通常被称为 ValueActor-Critic 算法，如式所示。

$${\nabla }_{\theta }J(\theta )\propto {\mathbb{E}}_{{\pi }_{\theta }}\left[V_{\omega }(s_t){\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)\right]$$

在参数更新方面，对于策略网络（ Actor ）的参数 𝜃 ，更新方式跟纯策略梯度算法类似，如式所示。

$$\begin{array}{r}\\ \theta \leftarrow \theta +\alpha V_{\omega }(s_i){\nabla }_{\theta }\log {\pi }_{\theta }(a_i|s_i)\end{array}$$

对于值函数网络（Critic），可以先计算时序差分误差的梯度表达式，然后利用该误差来更新值函数的参数，如式所示。

$${\nabla }_{\omega }L(\omega )=(r_t+\gamma V_{\omega }(s_{t+1})-V_{\omega }(s_t)){\nabla }_{\omega }{V}_{\omega }(s_t)$$

在上式基础上，我们可以通过梯度下降的方法来更新值函数的参数𝜔，如下式所示。

$$\begin{array}{rl}& \\ y_i& =r_i+\gamma V_{\omega }(s_{i+1})-V_{\omega }(s_i)\\ & \\ \omega & \leftarrow \omega +\beta y_i{\nabla }_{\omega }{V}_{\omega }(s_i)\end{array}$$

使用状态-动作值函数来表示Actor-Critic算法的形式通常被称为QActor-Critic算法，如式所示。

$${\nabla }_{\theta }J(\theta )\propto {\mathbb{E}}_{{\pi }_{\theta }}\left[Q_{\omega }(s,a){\nabla }_{\theta }\log {\pi }_{\theta }(a\mid s)\right]$$

同样地，Critic网络的参数𝜔也可以通过时序差分方法来更新，其梯度表达式如式所示。

$${\nabla }_{\omega }L(\omega )={\mathbb{E}}_{{\pi }_{\theta }}\left[(r_t+\gamma Q_{\omega }(s_{t+1},a_{t+1})-Q_{\omega }(s_t,a_t)){\nabla }_{\omega }{Q}_{\omega }(s_t,a_t)\right]$$

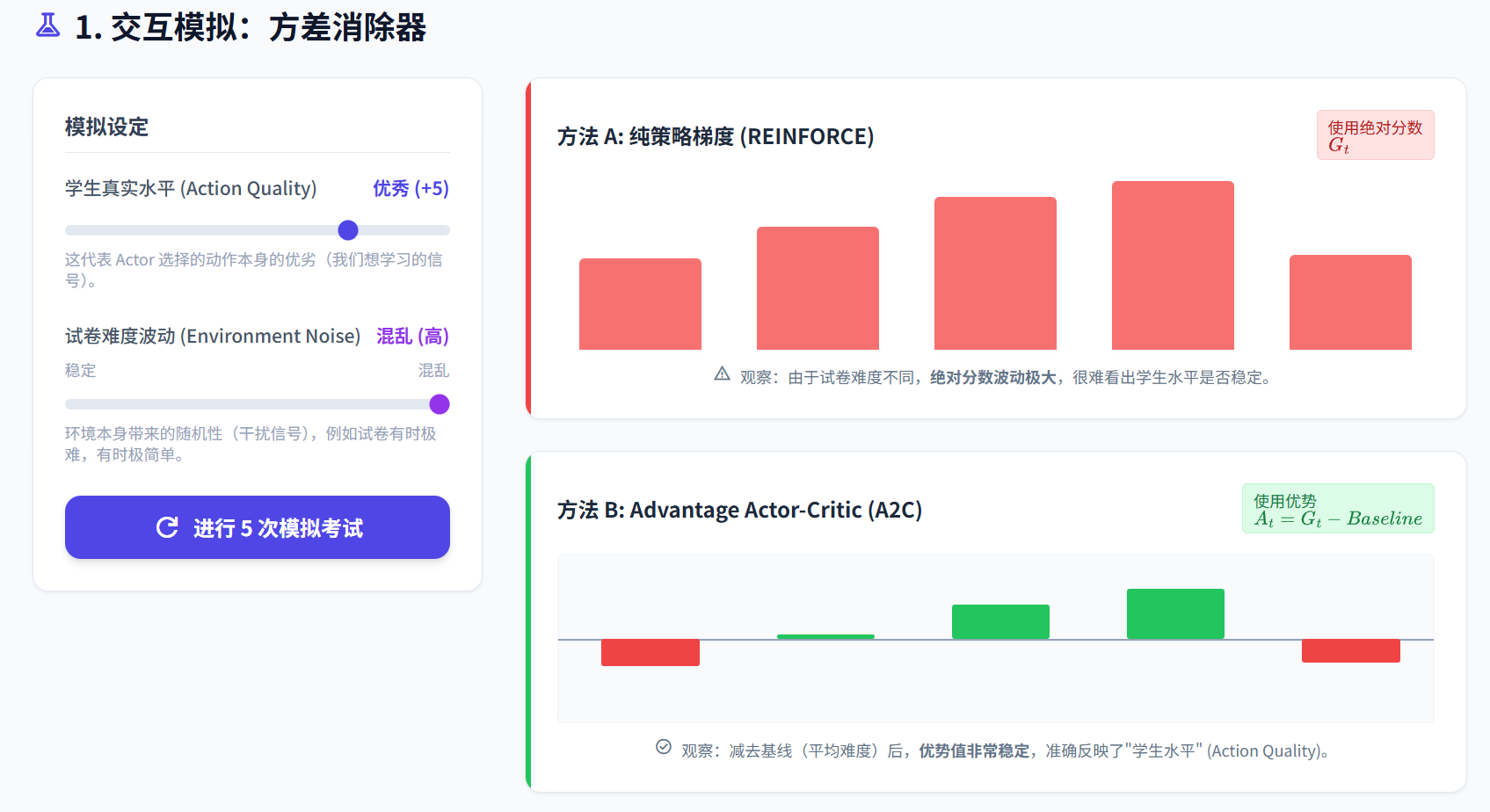
A2C算法

引入优势函数，进一步提高梯度估计的稳定性和准确性

$$A^{\pi }(s_t,a_t)=Q^{\pi }(s_t,a_t)-V^{\pi }(s_t)$$

相当于引入一个基线

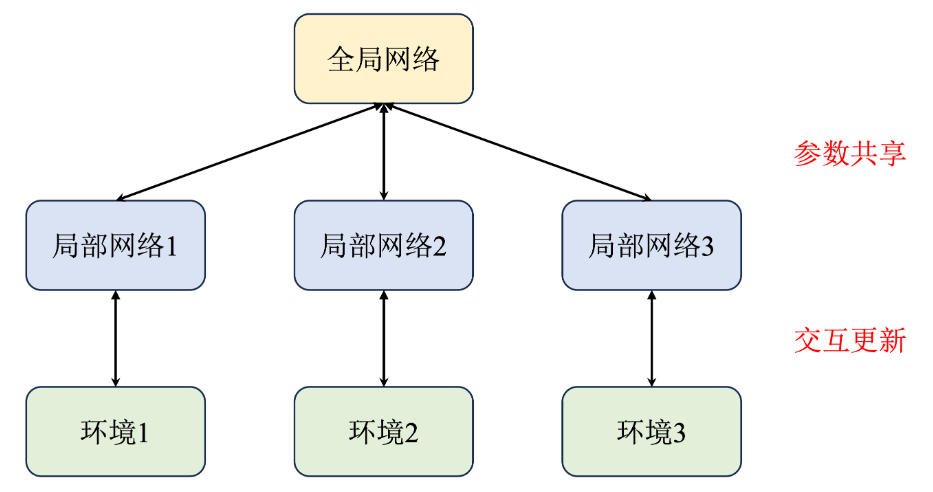
A3C算法

A3C算法通过引入多个并行的智能体（进程），每个智能体都拥有独立的策略和价值网络，并与环境进行交互采样数据。每个智能体在与环境交互一段时间后，会将其参数异步地更新到全局网络中，从而实现多进程的协同训练。

每一个智能体（进程）都拥有一个独立的网络和环境以供交互，并且每个进程每隔一段时间都会将自己的参数同步到全局网络中，这样就能提高训练效率。

参考文献

https://datawhalechina.github.io/joyrl-book/#/rl_basic/ch9/
https://datawhalechina.github.io/joyrl-book/#/rl_basic/ch10/