强化学习：DDPG算法、PPO算法、SAC算法

DDPG算法、PPO算法、SAC算法、阅读视觉强化学习/ICLR’25 Oral论文

DPG算法

使用确定性策略

确定性策略直接将状态映射到一个具体的动作，而不是一个概率分布，如式所示。

$$a={\mu }_{\theta }(s)$$

对应的策略梯度表达式如式所示。

$${\nabla }_{\theta }J(\theta )\approx {\mathbb{E}}_{s_t\sim {\rho }^{\beta }}\left[\underset{Q值随动作的变化率}{\underbrace{{\nabla }_{a}Q(s_t,a)}}{|}_{a={\mu }_{\theta }(s_t)}\cdot \underset{动作随网络参数的变化率}{\underbrace{{\nabla }_{\theta }{\mu }_{\theta }(s_t)}}\right]$$

这就是确定性策略梯度（DeterministicPolicyGradient，DPG）算法的核心，其中${\rho }^{\beta }$是策略的初始分布。

DDPG算法

基于DPG方法，DDPG算法在引入神经网络近似的同时，增加了一些要素，如式所示。

$$DDPG=DPG+\text{target network}+\text{experience replay}+\text{OU noise}$$

其中目标网络和经验回放在DQN算法中已经介绍过了，这里我们主要讲讲OU噪声，引入噪声的目的是为了增加策略的探索性，从而提高算法的性能和稳定性，如式所示。

$$d{x}_t=\theta (\mu -x_t)dt+\sigma d{W}_t$$

算法流程

TD3

连续动作空间表现好，但容易吹按Q值过估计问题。为了解决这个问题，TD3算法引入了双𝑄网络的概念，即使用两个独立的Critic网络来估计动作的价值。在计算目标值𝑦时，取两个𝑄值中的较小值作为目标值，从而减少过估计的风险，如式所示。

$$y=r+\gamma \underset{i=1,2}{\min }{Q}_{{\theta }_i^{\prime }}(s^{\prime },{\mu }_{{\varphi }^{\prime }}(s^{\prime }))$$

对应损失函数

$$L({\theta }_i)={\mathbb{E}}_{(s,a,r,s^{\prime })\sim D}\left[(Q_{{\theta }_i}(s,a)-y{)}^2\right]i=1,2$$

延迟更新

延迟更新（ DelayedPolicyUpdates ）是指在 TD3 算法中， Actor 网络的更新频率要低于 Critic 网络的更新频率。具体来说， Actor 网络每隔一定数量的时间步才会更新一次，而 Critic 网络则在每个时间步都进行更新。 这样做的目的是为了减少策略更新的频率，从而提高训练的稳定性。

目标策略平滑

目标策略平滑（TargetPolicySmoothing）是指在计算目标值𝑦时，给目标策略添加一些噪声，从而使得目标策略更加平滑，减少过估计的风险，也叫噪声正则（noiseregularization）。

我们也可以给Critic引入一个噪声提高其抗干扰性，这样一来就可以在一定程度上提高Critic的稳定性，从而进一步提高算法的稳定性和收敛性。

$$y=r+\gamma Q_{{\theta }^{\prime }}(s^{\prime },{\pi }_{{\varphi }^{\prime }}(s^{\prime })+ϵ)ϵ\sim \text{clip}(N(0,\sigma ),-c,c)$$

TRPO算法

基于策略的方法主要沿着策略梯度 ∇𝜃𝐽⁡(𝜃) 更新策略参数 𝜃 ，但是如果每次更新的步长过大，可能会导致策略发生剧烈变化，从而使得训练过程不稳定，甚至发散。 为了解决这个问题，TRPO（Trust Region Policy Optimization，信赖域策略优化）算法考虑在更新时引入一个约束，也叫做置信域（ TrustRegion ，用于限制每次更新后新旧策略之间的差异，从而保证策略更新的稳定性。

这张图沿着梯度方向更新参数，由于没有对更新步长进行限制，可能会导致参数更新过大，进而使得策略发生剧烈变化，偏离了最优的参数区域，导致训练不稳定。

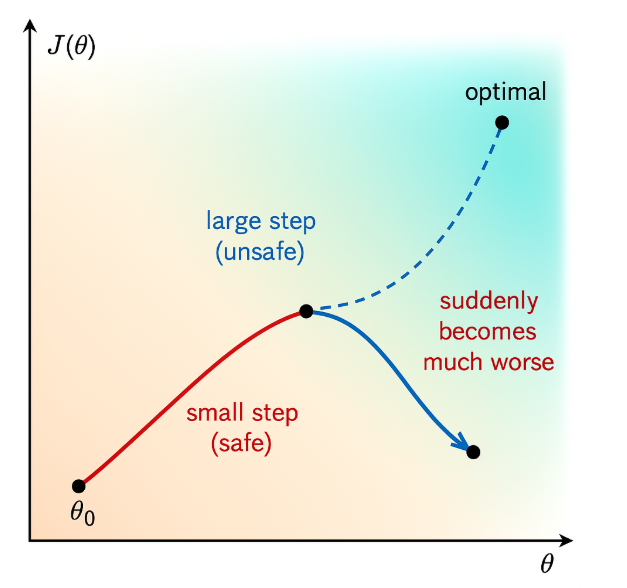
为了避免这种情况，TRPO 引入了置信域的概念，如下图所示，置信域定义了一个允许策略更新的区域，限制了新旧策略之间的差异，从而确保每次更新后的策略不会偏离旧策略太远。

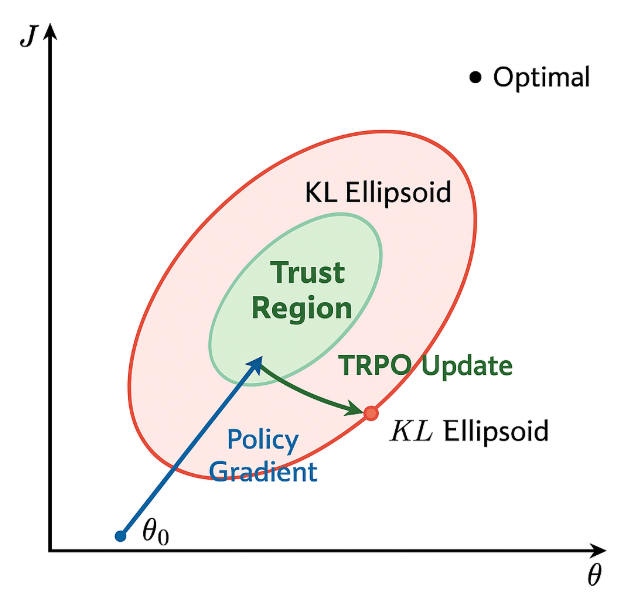
换句话说，在更新策略时，保证新策略${\pi }_{{\theta }_{\text{new}}}$和旧策略 ${\pi }_{{\theta }_{\text{old}}}$ 之间的差异不会太大，“一步一个脚印” 地优化策略，从而提高训练的稳定性。

置信域算法

在进入TRPO算法之前，我们来看下经典的置信域算法的简要步骤：

1） 给定初始参数𝜃， 确定约束邻域范围$N({\theta }_{\text{old}})$；
2） 寻找近似目标函数(approximation): $L(\theta |{\theta }_{\text{old}})$;
3） 最大化近似的目标函数(Maximation): ${\mathrm{argmax}}_{\theta \in N({\theta }_{old})}L(\theta |{\theta }_{old})$

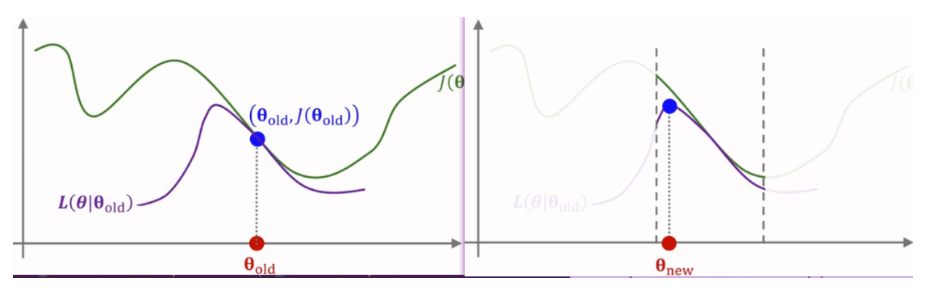
1） 给定初始参数 𝜃 ， 确定约束邻域范围$N({\theta }_{\text{old}})$ 。TRPO用KL散度来衡量新策略 ${\pi }_{{\theta }_{\text{new}}}$和旧策略 ${\pi }_{{\theta }_{\text{old}}}$之间的差异， 并做范围约束；

2） 寻找近似目标函数(approximation): $L(\theta |{\theta }_{\text{old}})$ 。一般强化学习都是对agent任务建模成奖励最大化问题（reward maximization）

$$\begin{array}{r}\\ {\mathrm{E}}_{\pi }[\tau (r)]=\sum _a^A{\pi }_{\theta }(a|s)Q(s,a)\end{array}$$

我们直接等价的加入旧策略

$$\begin{array}{r}\\ \sum _a^A{\pi }_{{\theta }_{\text{old }}}(a\mid s)\frac{{\pi }_{\theta }(a\mid s)}{{\pi }_{{\theta }_{\text{old }}}(a\mid s)}Q(s,a)={\mathbb{E}}_{a\sim {\pi }_{{\theta }_{\text{old }}}}\left[\frac{{\pi }_{\theta }(a\mid s)}{{\pi }_{{\theta }_{\text{old }}}(a\mid s)}Q(s,a)\right]\end{array}$$

可以直接用这个目标函数作为近似目标函数，即$L(\theta |{\theta }_{\text{old}})={\mathbb{E}}_{a\sim {\pi }_{{\theta }_{\text{old}}}}[\frac{{\pi }_{\theta }(a|s)}{{\pi }_{{\theta }_{\text{old}}}(a|s)}Q(s,a)]$

3） 约束范围内最大化(Maximation)

$$\underset{\theta \in N({\theta }_{\text{old}})}{\mathrm{argmax}}L(\theta |{\theta }_{\text{old}})$$

上述方法存在最后一个问题，无法保证每次迭代都朝着优化方向前进。为了达到迭代时保证策略性能单调递增， 我们可以用baseline的方法将 𝑄⁡(𝑠,𝑎) 替成优势函数 𝐴⁡(𝑠,𝑎) （见证明1）。所以最后的近似目标函数可以变成如下：

$$L(\theta |{\theta }_{\text{old}})={\mathbb{E}}_{a\sim {\pi }_{{\theta }_{\text{old}}}}[\frac{{\pi }_{\theta }(a|s)}{{\pi }_{{\theta }_{\text{old}}}(a|s)}A(s,a)]$$

PPO算法

PPO算法是一类典型的Actor-Critic算法，既适用于连续动作空间，也适用于离散动作空间。

PPO 算法是一种基于策略梯度的强化学习算法，由 OpenAI 的研究人员 Schulman 等人在 2017 年提出。 PPO 算法的主要思想是通过在策略梯度的优化过程中引入一个重要性权重来限制策略更新的幅度，从而提高算法的稳定性和收敛性。 PPO 算法的优点在于简单、易于实现、易于调参，应用十分广泛，正可谓 “遇事不决 PPO ”。

重要性采样

设有一个函数𝑓⁡(𝑥)，需要从分布𝑝⁡(𝑥)中采样来计算其期望值，但是在某些情况下我们可能很难从𝑝⁡(𝑥)中采样，这个时候我们可以从另一个比较容易采样的分布𝑞⁡(𝑥)中采样，来间接地达到从𝑝⁡(𝑥)中采样的效果。

$$E_{p(x)}[f(x)]={\int }_a^{b}f(x)\frac{p(x)}{q(x)}q(x)dx=E_{q(x)}\left[f(x)\frac{p(x)}{q(x)}\right]$$

对于离散分布的情况，可以表达为下式

$$E_{p(x)}[f(x)]=\frac{1}{N}\sum f(x_i)\frac{p(x_i)}{q(x_i)}$$

PPO算法的核心思想就是通过重要性采样来优化原来的策略梯度估计，其目标函数表示如式所示。

$$\begin{array}{rl}& \\ J^{\text{TRPO}}(\theta )& =\mathbb{E}\left[r(\theta ){\hat{A}}_{{\theta }_{\text{old}}}(s,a)\right]\\ & \\ r(\theta )& =\frac{{\pi }_{\theta }(a|s)}{{\pi }_{{\theta }_{\text{old}}}(a|s)}\end{array}$$

换句话说，本质上PPO算法就是在Actor-Critic算法的基础上增加了重要性采样的约束而已，从而确保每次的策略梯度估计都不会过分偏离当前的策略，也就是减少了策略梯度估计的方差，从而提高算法的稳定性和收敛性。

$$J^{\text{TRPO}}(\theta )=E_{(s_t,a_t)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^{\prime }}(a_t|s_t)}{A}^{{\theta }^{\prime }}(s_t,a_t)\nabla \log p_{\theta }(a_t^n|s_t^n)\right]$$

SAC算法

确定性策略和随机性策略，确定性策略是指在给定相同状态下，总是选择相同的动作，随机性策略则是在给定状态下可以选择多种可能的动作，不知道读者们有没有想过这两种策略在实践中有什么优劣呢？或者说哪种更好呢？这里我们先架空实际的应用场景，只总结这两种策略本身的优劣，首先看确定性策略：

优势：稳定性且可重复性。由于策略是确定的，因此可控性也比较好，在一些简单的环境下，会更容易达到最优解，因为不会产生随机性带来的不确定性，实验也比较容易复现。

劣势：缺乏探索性。由于策略是确定的，因此在一些复杂的环境下，可能会陷入局部最优解，无法探索到全局最优解，所以读者会发现目前所有的确定性策略算法例如DQN、DDPG等等，都会增加一些随机性来提高探索。此外，面对不确定性和噪音的环境时，确定性策略可能显得过于刻板，无法灵活地适应环境变化。

再看看随机性策略：

优势：更加灵活。由于策略是随机的，这样能够在一定程度上探索未知的状态和动作，有助于避免陷入局部最优解，提高全局搜索的能力。在具有不确定性的环境中，随机性策略可以更好地应对噪音和不可预测的情况。

劣势：不稳定。正是因为随机，所以会导致策略的可重复性太差。另外，如果随机性太高，可能会导致策略的收敛速度较慢，影响效率和性能。

我们先回顾一下标准的强化学习框架，其目标是得到最大化累积奖励的策略，如式所示。

$${\pi }^{\ast }=\arg \underset{\pi }{\max }\sum _t{\mathbb{E}}_{({\mathbf{s}}_t,{\mathbf{a}}_t)\sim {\rho }_{\pi }}\left[{\gamma }^{t}r({\mathbf{s}}_t,{\mathbf{a}}_t)\right]$$

而最大熵强化学习则是在这个基础上加上了一个信息熵的约束，如式所示。

$${\pi }_{\text{MaxEnt}}^{\ast }=\arg \underset{\pi }{\max }\sum _t{\mathbb{E}}_{\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\sim {\rho }_{\pi }}\left[{\gamma }^t\left(r\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)+\alpha \mathcal{H}\left(\pi \left(\cdot \mid {\mathbf{s}}_t\right)\right)\right)\right]$$

其中𝛼是一个超参，称作温度因子（temperature），用于平衡累积奖励和策略熵的比重。这里的$\mathcal{H}\left(\pi \left(\cdot \mid {\mathbf{s}}_t\right)\right)$就是策略的信息熵，定义如式所示。

$$\mathcal{H}\left(\pi \left(\cdot \mid {\mathbf{s}}_t\right)\right)=-\sum _{{\mathbf{a}}_t}\pi \left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)\log \pi \left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)$$

SAC有两个版本

第一版算法思想基本上是和SoftQ-Learning是⁢特⁢别⁢相⁢似⁢的，只⁢是⁢额⁢外⁢增⁢加⁢了⁢两⁢个V值⁢网⁢络⁡（即⁢包⁢含⁢目⁢标⁢网⁢络⁡和⁢当⁢前⁢网⁢络）⁢来⁢估⁢计⁢价⁢值。

$$J_V(\psi )={\mathbb{E}}_{{\mathbf{s}}_t\sim \mathcal{D}}\left[\frac{1}{2}{\left(V_{\psi }({\mathbf{s}}_t)-{\mathbb{E}}_{{\mathbf{a}}_t\sim {\pi }_{\varphi }}\left[Q_{\theta }({\mathbf{s}}_t,{\mathbf{a}}_t)-\log {\pi }_{\varphi }({\mathbf{a}}_t\mid {\mathbf{s}}_t)\right]\right)}^2\right]$$

梯度

$$\begin{array}{r}\\ {\hat{\nabla }}_{\psi }{J}_V(\psi )={\nabla }_{\psi }{V}_{\psi }({\mathbf{s}}_t)(V_{\psi }({\mathbf{s}}_t)-Q_{\theta }({\mathbf{s}}_t,{\mathbf{a}}_t)+\log {\pi }_{\varphi }({\mathbf{a}}_t\mid {\mathbf{s}}_t))\end{array}$$

参考文献

https://datawhalechina.github.io/joyrl-book/#/rl_basic/ch11/