编程题-二叉树的中序遍历

题目：

给定一个二叉树的根节点 root ，返回 它的 中序 遍历。

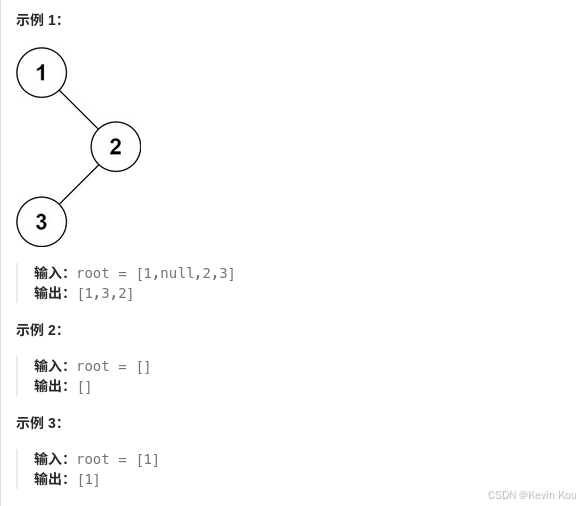
解答一（递归）：

首先我们需要了解什么是二叉树的中序遍历：按照访问左子树——根节点——右子树的方式遍历这棵树，而在访问左子树或者右子树的时候我们按照同样的方式遍历，直到遍历完整棵树。因此整个遍历过程天然具有递归的性质，我们可以直接用递归函数来模拟这一过程。如下为笔者代码：

class Solution {
public:
    //定义返回值为result
    vector<int> result;
    vector<int> inorderTraversal(TreeNode* root) {
        TreeNode* current = root;
        //判断当前指针是否为空，为空则直接返回函数
        if(current==nullptr){
            return result;
        }
        //先遍历左子树，遍历完成后添加根节点的值，随后再遍历右子树
        if(current->left!=nullptr){
            inorderTraversal(current->left);
            result.push_back(current->val);
            if(current->right!=nullptr){
                inorderTraversal(current->right);
            }
        }
        else{
            result.push_back(current->val);
            if(current->right!=nullptr){
                inorderTraversal(current->right);
            }
        }
        return result;
    }
};

解答二（迭代）：

方法一的递归函数我们也可以用迭代的方式实现，两种方式是等价的，区别在于递归的时候隐式地维护了一个栈，而我们在迭代的时候需要显式地将这个栈模拟出来，其他都相同，具体实现可以看下面的代码。代码如下所示：

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        //创建函数返回值res
        vector<int> res;
        //创建元素类型为TreeNode的显示栈stk
        stack<TreeNode*> stk;
        //当root不为空，或者stk不为空时，执行第一层while循环
        while (root != nullptr || !stk.empty()) {
            //当root不为空时，将root入栈，并将root赋值为原root的左子树，直至root为空
            while (root != nullptr) {
                stk.push(root);
                root = root->left;
            }
            //访问stk栈顶元素，将其地址赋值给root，并清除栈顶元素，将root根节点值压入容器res中
            root = stk.top();
            stk.pop();
            res.push_back(root->val);
            //root赋值给原root的右子树，并执行重新执行while循环，直至stk栈为空时结束循环
            root = root->right;
        }
        return res;
    }
};

特别需要注意：在二叉树中序遍历时：在递归的时候栈是隐式地维护的，在迭代的时候栈是显示的维护模拟出来。