数论基础——数论函数(1)

最新推荐文章于 2023-03-17 11:37:53 发布

雨潇ヽ

最新推荐文章于 2023-03-17 11:37:53 发布

阅读量4.1k

点赞数 1

CC 4.0 BY-SA版权

分类专栏：数论

本文链接：https://blog.youkuaiyun.com/qq_43280520/article/details/103375715

数论专栏收录该内容

21 篇文章

订阅专栏

本文深入介绍了数论函数，包括因子个数、素因子个数、Euler函数、Möbius函数等，并探讨了Dirichlet乘积、积性函数和它们的变换与反变换。通过理解这些概念，可以更好地掌握数论中的计算和理论。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

**内含学习莫比乌斯所必须的数论函数，Dirichlet乘积（以及广义），莫比乌斯函数，欧拉函数，积性函数，莫比乌斯变换及反变换。

1.数论函数举例

定义1：在全体正整数（或者整数）上定义的函数称作数论函数或是算术函数。

也就是说只要定义在整数上面的函数都是数论函数咯？终于明白数论函数是个什么鬼东东

下面是定义在全体自然数集合上的数论函数

1)

常函数：

u(n)≡1 n≥1

单位函数：

e(n)=n n≥1

单位元（幺元）：

$I(n)=\left\{\begin{matrix}1, & n=1, \\ 0, & n>1. \end{matrix}\right.$

以下2~4均是建立在算数基本定理即数字的质因数分解之上

2)因子个数

n=p1^a1*p2^a2*p3^a3……

n的所有正除数的个数d(n)=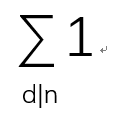=（a1+1)(a2+1)(a3+1)……

此为算法中，求解一个数的因子的个数的由来。

证明过程：

n=p1^a1*p2^a2*p3^a3

所以任意n的正除数一定也是由这几个p构成。已知p的指数，每一个除数都可以选择指数+1种数字作为pi的指数，所以一共有d(n)个。

通常我们称d(n)为除数函数。

3）全部素因子个数

n的全部素因子的个数（按重数计）Ω(n)

Ω(1)=0

Ω(n)=a1+a2+a3+……+as

4）不同素因子个数

n的不同素因子的个数ω(n)

ω(1)=0;

ω(n)=s;

5)额

n的正整数的幂和函数σλ(n)，λ为实数

σλ(n)=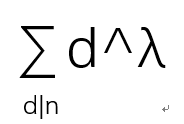

不知道是个啥玩意，搜百度也找不到

6）Euler函数

所有不超过n的与n互质的数的个数φ(n)，称为Euler函数。

相当的重要，做过的题也不少了，Euler函数一直会变着法子考你

重点代码为：

res=res/i*(i-1);

7)Mоbius函数μ(n)

8）Mangoldt函数 $\wedge$ (n)

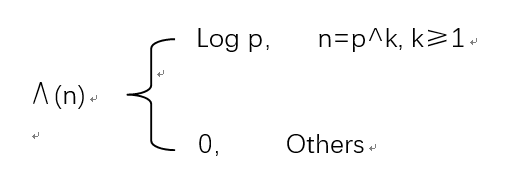
9)Liouville函数λ(n)

λ(n)=(-1)^Ω(n)

注：Ω(n)是上方的素因子个数的函数

2 Dirichlet乘积

原来它只是对数论函数的一个运算而已！！！

数论函数有种重要的运算称作Dirichlet乘积或者卷积，其定义如下：

定义2：设f(n),g(n)是两个数论函数，则

$h(n)=\sum_{d|n}^{ }f(d)g(\frac{n}{d})$

称为f(n)或是g(n)的Dirichlet乘积或是卷积，记作

$h=f*g$

好看一点就是 $h(n)=\sum_{ab=n}^{ }f(a)g(b)$

定理1：设f,g,h为任意三个数论函数，则

$f*g=g*f$

$(f*g)*h=f*(g*h)$

$\Rightarrow$ 满足结合律和交换律

下面为莫比乌斯函数一个重要的性质，是Dirichlet卷积的结果

由Dirichlet我们可以进行一些有意思的推导，比如：

$I(n)=\left\{\begin{matrix}1, & n=1, \\ 0, & n>1. \end{matrix}\right.$ 等于莫比乌斯函数 $\mu (n)$ 和 $u(n)\equiv 1$ 的乘积，I(n)就是单位元（离散数学里面刚刚学的幺元！！！激动！！）。

即

$I=\mu *u$

根据幺元的性质，他俩是互为逆元的。

所以 $I(n)$ 就是 $M\ddot{o}bius$ 函数的 $M\ddot{o}bius$ 变换，下面会有这个性质

得

$\sum_{d|n}^{ }\mu (d)\left\{\begin{matrix}1, & n=1, \\ 0, & n>1. \end{matrix}\right.$

我可以证明他成立，但是不知道他是怎么写出来的？

证明过程：

$\sum_{d|n}^{ }\mu (d)=\mu(1) +\mu(p_{1}) +\cdots +\mu(p_{s})+\mu (p_{1}p_{2})+\cdots +\mu (p_{s-1}p_{s})+\cdots +\mu (p_{1}p_{2}\cdots p_{s})=\sum_{i=0}^{k}\textrm{C}_{k}^{i}\cdot (-1)^{k}$

由二项式定理

$\sum _{i=1}^{n}C_{n}^{k}x^{k}y^{n-k}=(x+y)^{n}$

得此公式的解为

$(1-1)^{s}$

由此得出，除了当s=0时（即n=1时）可以得到1以外，其他的情况答案均为0。

证毕。

定义3：设f(n)为数论函数，若存在一个数论函数g(n)使得

$f*g=I$

则称g(n)为f(n)的Dirichlet逆，记作 $f^{-1}(n)$

定理2： $I$ 为卷积中的单位元（单位元是不是唯一来着？），即

$f*I=I*f=f$

证： $(f*I)(n)=\sum_{d|n}^{ }f(d)I(\frac{n}{d})=f(n)$

第一步是因为Dirichlet的定义式

第二部是因为 $I$ 是单位元，除了1之外都是0，巧的是n除以n的约数一直是1鸭（你说巧不巧？）

定义4：

( $u(n)$ 是常数函数来着)

若 $F=f*u$ 则称 $F$ 为 $f$ 的M $\ddot{o}$ bius变换,亦即

$F(n)=\sum_{d|n}^{ }f(d)$

例如：

$d(n)$ 为 $u(n)$ 的 $M\ddot{o}bius$ 变换，所以当时的 $d(n)=\sum_{d|n}1$ 啊

而 $I(n)$ 为 $\mu (n)$ 的 $M\ddot{o}bius$ 变换

定理3：若 $F=f*u$ ，则 $f=F*\mu$ .

证： $F*u=(f*u)*\mu =f*(u*\mu )=f*I=f$

定理3表明，若

$F(n)=\sum_{d|n}f(d)$

则

$f(n)=\sum_{d|n}F(d)\mu (\frac{n}{d})$

此时我们称 $f$ 为 $F$ 的 $M\ddot{o}bius$ 反变换。

$M\ddot{o}bius$ 反变换唯一

证明：

设 ${f}'$ 也是F的 $M\ddot{o}bius$ 反变换，则

${f}'=F*\mu =(f*u)*\mu =f*(u*\mu )=f*I=f$

矛盾

反变换唯一

$M\ddot{o}bius$ 反演：

如果 $f$ 与 $F$ 是 $M\ddot{o}bius$ 函数

所进行的反变换行为被称作 $M\ddot{o}bius$ 反演。

$M\ddot{o}bius$ 变换的例子：

1）e(n)为欧拉函数 $\varphi (n)$ 的 $M\ddot{o}bius$ 变换

即 $n=\sum_{d|n}\varphi (d)=\sum_{d|n}\varphi (\frac{n}{d})$

由定理3 $M\ddot{o}bius$ 反变换可知：

$\varphi (n)=\sum _{d|n}\mu (d) (\frac{n}{d})$

2) $log n$ 为Mangoldt函数 $\Lambda(n)$ 的 $M\ddot{o}bius$ 变换

即 $log n=\sum_{d|n}\Lambda (d)$

由定理3得：

$\Lambda (n)=\sum _{d|n}\mu (d)log(\frac{n}{d})$

关于 $M\ddot{o}bius$ 函数以及 $M\ddot{o}bius$ 变换和 $M\ddot{o}bius$ 反变换的应用，本小可爱还在思索，于是决定看一下博客，首先强化一下对 $M\ddot{o}bius$ 函数的深刻理解，其次是了解题型，懂得最简单的应用，最后是熟悉模板，了解如何从理论化为实践。