逻辑回归整理

随机梯度下降的逻辑回归代码

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris

ld = load_iris()
x_data = ld.data
y_target = ld.target
y_train = y_target[y_target != 2]
a = []
for i, j in enumerate(y_train):
    a.append(x_data[i])

x_train = pd.DataFrame(a)


class logistic_regression():

def fit(self, x_train, y_train, k=200):
    self.x_train = x_train
    self.y_train = y_train
    self.k = k

def sigmoid(self, inx):
    return 1 / (1 + np.exp(-inx))

def logistic_regression_model(self):
    x_train_1 = np.array(self.x_train)
    y_train_1 = np.array(self.y_train)
    weights = np.ones(np.shape(x_train_1)[1])
    alpha = 0.0001
    for j in range(self.k):
        for i in range(np.shape(x_train_1)[0]):
            h = self.sigmoid(np.sum(x_train_1[i] * weights))
            error = h - y_train_1[i]
            weights = weights - alpha * error * x_train_1[i]
    return weights

def predict(self, x_test):
    x_test = np.array(x_test)
    weights_ = self.logistic_regression_model()
    y_predict = []
    for k in range(np.shape(x_test)[0]):
        result = self.sigmoid(np.sum(x_test[k] * weights_))
        if result > 0.5:
            result_1 = 1
            y_predict.append(result_1)
        else:
            result_2 = 0
            y_predict.append(result_2)
    return y_predict


a = logistic_regression()
a.fit(x_train, y_train)
print(a.predict(x_train))

sigmord 函数求导

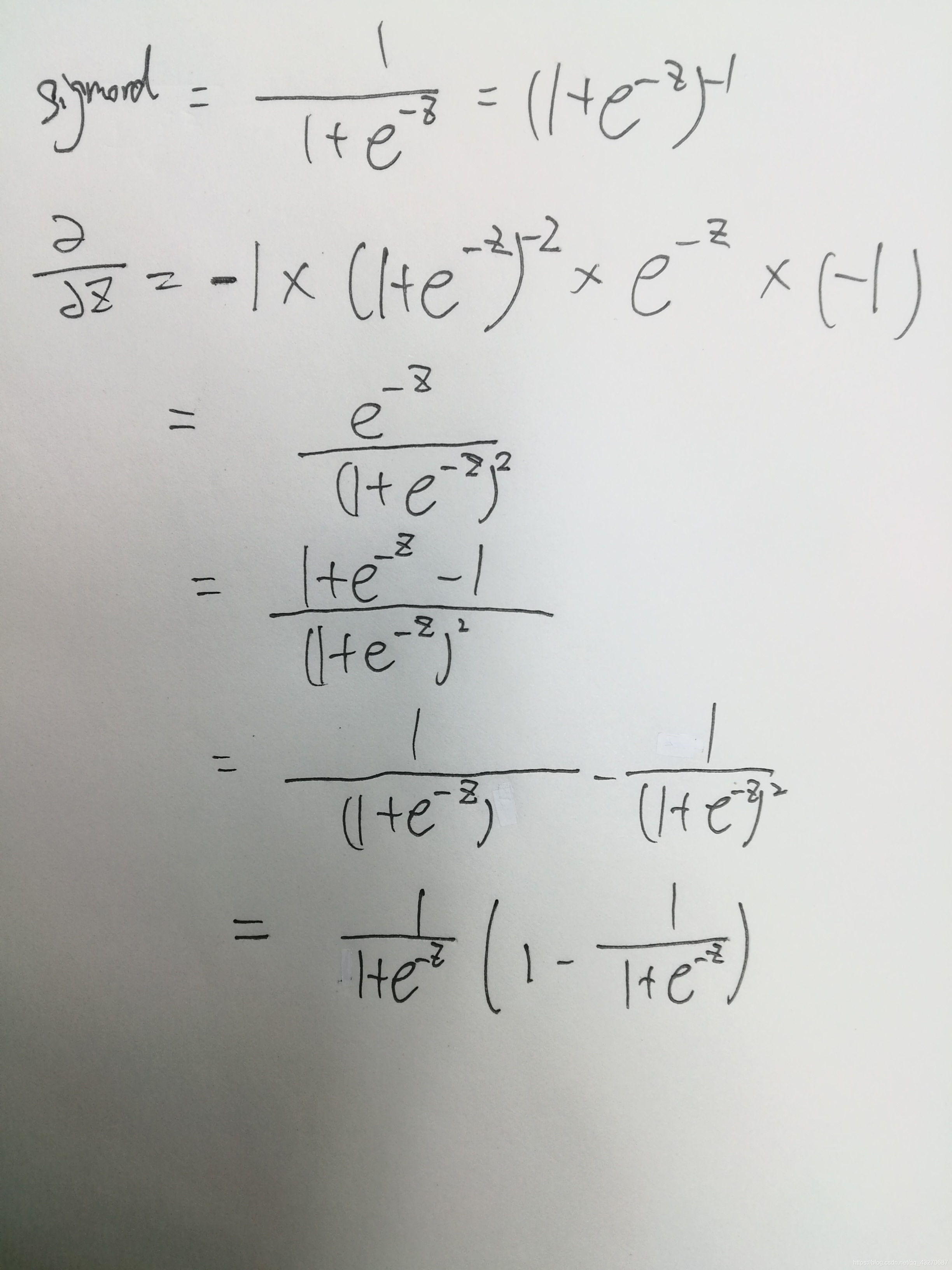
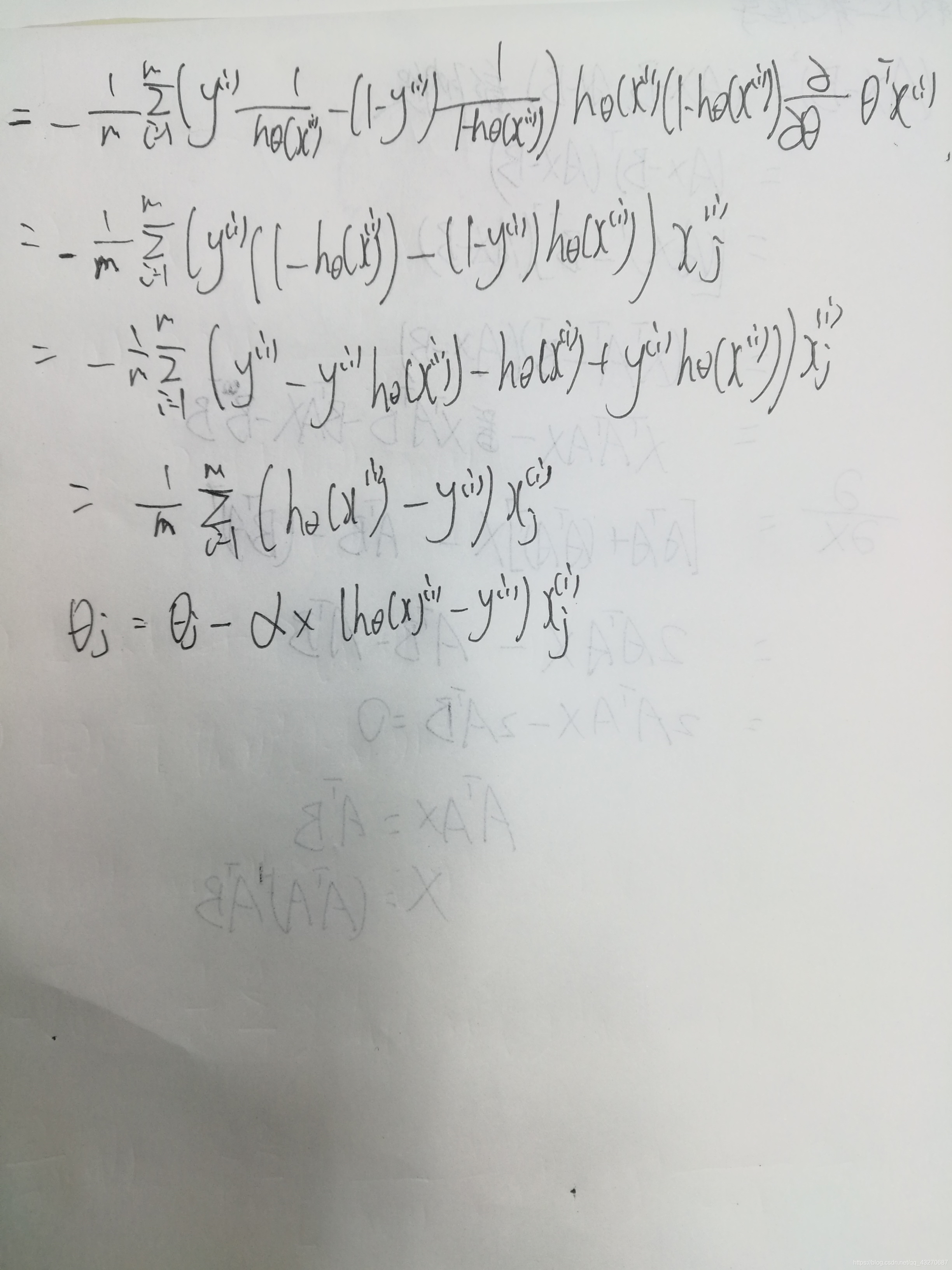
逻辑回归到底属于分类还是回归？

分类。只是很多时候，对于逻辑回归的某些应用场合，最终要的结果可能不是分类的结果，而是计算出的概率。这里可能会混淆认知。