Robust PCA

Robust PCA

Rachel Zhang

 

1. RPCA Brief Introduction

1.     Why use Robust PCA?

Solve the problem withspike noise with high magnitude instead of Gaussian distributed noise.

2.     Main Problem

Given C = A*+B*, where Ais a sparse spike noise matrix and B is a Low-rank matrix, aiming at recoveringB*.

B*= UΣV’, in which U∈R^nk ,Σ∈R^kk ,V∈R^nk

3.     Difference from PCA

Both PCA and Robust PCAaims at Matrix decomposition, However,

In PCA, M = L0+N0,    L0:low rank matrix ; N0: small idd Gaussian noise matrix,it seeks the best rank-k estimation of L0 by minimizing ||M-L||₂ subjectto rank(L)<=k. This problem can be solved by SVD.

In RPCA, M = L0+S0, L0:low rank matrix ; S0: a sparse spikes noise matrix, we’lltry to give the solution in the following sections.

 

2. Conditionsfor correct decomposition

4.     Ill-posed problem:

Suppose sparse matrix A and B*=e_ie_j^Tare the solution of this decomposition problem.

1)       With the assumption that B* is not only low rank but alsosparse, another valid sparse-plus low-rank decomposition might be A₁= A*+ e_ie_j^T andB₁ = 0, Therefore, we need an appropriatenotion of low-rank that ensures that B* is not too sparse. Conditionswill be imposed later that require the space spanned by singular vectors U andV (i.e., the row and column spaces of B*) to be “incoherent” with the standardbasis.

2)       Similarly, with the assumption that A* is sparse as well aslow-rank (e.g. the first column of A* is non-zero, while all other columns are0, then A* has rank 1 and sparse). Another valid decomposition might be A₂=0,B₂ = A*+B* (Here rank(B₂) <= rank(B*) + 1). Thus weneed the limitation that sparse matrix should beassumed not to be low rank. I.e., assume each row/column does not havetoo many non-zero entries (don’t exist dense row/column), to avoid such issues.

5.     Conditions for exact recovery / decomposition:

If A* and B* are drawnfrom these classes, then we have exact recovery with high probability [1].

1)       For low rank matrix L—Random orthogonal model [Candes andRecht 2008]:

A rank-k matrix B* with SVD B*=UΣV’ is constructed in this way: Thesingular vectors U,V∈R^nk are drawnuniformly at random from the collection of rank-k partial isometries(等距算子) inR^nk. The singular vectors in U and V need not be mutuallyindependent. No restriction is placed on the singular values.

2)       For sparse matrix S—Random sparsity model:

The matrix A* such that support(A*) is chosen uniformlyat random from the collection of all support sets of size m. There is noassumption made about the values of A* at locations specified by support(A*).

[Support(M)]: thelocations of the non-zero entries in M

Latest [2] improved on the conditions andyields the ‘best’ condition.

 

3. Recovery Algorithms

6.     Formulization

For decomposition D = A+E,in which A is low rank and error E is sparse.

1)       Intuitively propose

minrank(A)+γ||E||₀,    (1)

However, it is non-convex thus intractable (both of these 2are NP-hard to approximate).

2)       Relax L0-norm to L1-norm and replace rank with nuclear norm

min||A||_* + λ||E||₁,

where||A||_* =Σ_iσ_i(A)   (2)

        This is convex, i.e., exist a uniquely minimizer.

Reason: This relaxation ismotivated by observing that ||A||_* + λ||E||₁ is theconvex envelop (凸包) of rank(A)+γ||E||₀ over the set of (A,E) suchthat max(||A||_2,2,||E||_{1, ∞})≤1.

Moreover, there might be circumstancesunder which (2) perfectly recovers low-rank matrix A₀.[3] shows itis indeed true under surprising broad conditions.

 

7.     Approach RPCA Optimization Algorithm

We approach in twodifferent ways. 1^st approach, use afirst-order method to solve the primal problem directly. (E.g. ProximalGradient, Accelerated Proximal Gradient (APG)), the computational bottleneck ofeach iteration is a SVD computation. 2^ndapproach is to formulate and solve the dual problem, and retrieve the primalsolution from the dual optimal solution. The dual problem too RPCA canbe written as:

max_Ytrace(D^TY) , subject to J(Y) ≤ 1

where J(Y) = max(||Y||₂,λ^-1||Y||_∞). ||A||_x means the x norm of A.(无穷范数表示矩阵中绝对值最大的一个)。This dual problem can besolved by constrained steepest ascent.

Now let’s talk about Augmented Lagrange Multiplier (ALM) and Alternating Directions Method (ADM) [2,4].

7.1. General method of ALM

For the optimizationproblem

min f(X), subj. h(X)=0     (3)

we can define the Lagrangefunction:

L(X,Y,μ) = f(X)+<Y, h(x)>+μ/2||h(X)|| _F²       (4)

where Y is a Lagrangemultiplier and μ is a positive scalar.

General method of ALM is:

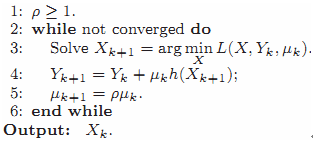
A genetic Lagrangemultiplier algorithm would solve PCP(principle component pursuit) by repeatedlysetting (X_k) = arg min L(X_k,Y_k,μ), and then the Lagrangemultiplier matrix via Y_k+1=Y_k+μ(h_k(X))

 

7.2  ALM algorithm for RPCA

In RPCA, we can define (5)

X = (A,E), f(x) = ||A||_* + λ||E||₁, andh(X) = D-A-E

Then the Lagrange functionis (6)

L(A,E,Y, μ) = ||A||_* + λ||E||₁+ <Y, D-A-E>+μ/2·|| D-A-E || _F ²

The Optimization Flow is just like the general ALM method. The initialization Y= Y₀* isinspired by the dual problem(对偶问题) as it is likely to make the objective function value <D,Y₀> reasonably large.

 

Theorem 1.  For algorithm 4, any accumulation point (A,E*) of (A_k, E_k)is an optimal solution to the RPCA problem and the convergence rate is at least O(μ_k^-1).[5]

Inthis RPCA algorithm, a iteration strategy is adopted. As the optimizationprocess might be confused, we impose 2 well-known facts: (7)(8)

Sε[W] = arg min_X ε||X||₁+ ½||X-W||_F^{2       （7）}

U Sε[W] V^T = arg min_X ε||X||_*+½||X-W||_F^{2        （8）}

which is used in the abovealgorithm for optimization one parameter while fixing another. In thesolutions, Sε[W] is the soft thresholding operator. Here I will impose the problemto speculate this. (To facilitate writing formulation and ploting, I use amanuscript. )

BTW,S_u(x) is easily implemented by 2 lines:

S_u(X)= max(x-u , 0);

S_u(X)= S_u(X) + min(X+u , 0);

 

 

 

Now we utilize formulation (7,8) into RPCA problem.

For the objective function (6) w.r.t get optimal E, wecan rewrite the objective function by deleting unrelated component into:

f(E) = λ||E||₁+ <Y, D-A-E> +μ/2·|| D-A-E|| _F ²

       =λ||E||₁+ <Y, D-A-E> +μ/2·||D-A-E || _F ²+(μ/2)||μ^-1Y||²//add an irrelevant item w.r.t E

       =λ||E||₁+(μ/2)(2(μ^-1Y· (D-A-E))+|| D-A-E || _F ²+||μ^-1Y||²) //try to transform into (7)’s form

       =(λ/μ)||E||1+½||E-(D-A-μ^-1Y)||_F²

Finally we get the form of (7) and in the optimizationstep of E, we have

E = S_λ/μ[D-A-μ^-1Y]

,same as what mentioned in algorithm 4.

Similarly, for matrices X, we can prove A=US_1/μ(D-E-μ^-1Y)V is theoptimization process of A.

 

 

8. Experiments 

 Here I’ve tested on a video data. This data is achieved from a fixed point camera and the scene is same at most time, thus the active variance part can be regarded as error E and the stationary/invariant part serves as low rank matrix A. The following picture shows the result. As the person walks in, error matrix has its value. The 2 subplots below represent low rank matrix and sparse one respectively. 

 

9.     Reference:

1)       E. J. Candes and B. Recht. Exact Matrix Completion Via ConvexOptimization. Submitted for publication, 2008.

2)       E. J. Candes, X. Li, Y. Ma, and J. Wright. Robust PrincipalComponent Analysis Submitted for publication, 2009.

3)       Wright, J., Ganesh, A., Rao, S., Peng, Y., Ma, Y.: Robustprincipal component analysis: Exact recovery of corrupted low-rank matrices viaconvex optimization. In: NIPS 2009.

4)       X. Yuan and J. Yang. Sparse and low-rank matrix decompositionvia alternating direction methods. preprint, 2009.

5)       Z. Lin, M. Chen, L. Wu, and Y. Ma. The augmented Lagrangemultiplier method for exact recovery of a corrupted low-rank matrices.Mathematical Programming, submitted, 2009.

6)       Generalized Power method for Sparse Principal Component Analysis

 

 

本文尚不成熟，希望大家提出宝贵意见。

关于Machine Learning更多的学习资料与相关讨论将继续更新，敬请关注本博客和新浪微博Rachel____Zhang.
。