python计算机视觉——相机标定之张正友标定法

1. 相机标定的目的

1.1 相机的成像原理

相机成像系统中，共包含四个坐标系：世界坐标系、相机坐标系、图像坐标系、像素坐标系。

这四个坐标系之间的转化关系为：

其中，（U,V,W）为在世界坐标系下一点的物理坐标， (u,v) 为该点对应的在像素坐标系下的像素坐标， Z 为尺度因子。我们将矩阵：

称为相机的内参矩阵，内参矩阵取决于相机的内部参数。其中，f 为像距，dX,dY别表示X,Y方向上的一个像素在相机感光板上的物理长度（即一个像素在感光板上是多少毫米），u0，v0分别表示相机感光板中心在像素坐标系下的坐标，θ 表示感光板的横边和纵边之间的角度（90°表示无误差）。

将矩阵
称为相机的外参矩阵，外参矩阵取决于相机坐标系和世界坐标系的相对位置，R表示旋转矩阵T，表示平移矢量。
即无畸变的相机成像模型如下：

1.2 相机标定的目的

当我们拿到一张图片，进行识别之后，得到的两部分之间的距离为多少多少像素，但是这多少多少像素究竟对应实际世界中的多少米呢？这就需要利用相机标定的结果来将像素坐标转换到物理坐标来计算距离（当然这里值得说明，仅仅利用单目相机标定的结果，是无法直接从像素坐标转化到物理坐标的，因为透视投影丢失了一个维度的坐标，所以测距其实需要双目相机）。

相机标定的目的其实很简单，我们要想对一个成像系统建模，进而进行相应的计算，所必须的参数就是相机的内参矩阵和相机的外参矩阵，因此，相机标定的第一个目的就是获得相机的内参矩阵和外参矩阵。

1.3 畸变与畸变矫正

另外，相机拍摄的图片还存在一定的畸变，畸变包括桶形畸变和枕形畸变。

由于径向畸变，直线会变弯。距离图片中心越远，它的影响越大。如下面这张图片，棋盘格中被红线标记的边缘。你会发现棋盘格的边缘并不与直红线重合，而是变弯了。可以到维基百科查看更多细节Distortion (optics) 。



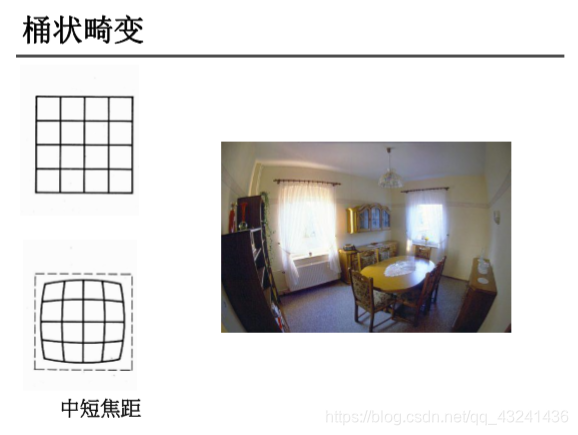
畸变模型包括径向畸变和切向畸变。
径向畸变公式（3阶）如下：

切向畸变公式如下：

其中，$(x,y)(\hat{x},\hat{y}$