BIOS14: ONE-WAY ANOVA(单因素方差分析) using R

NOTES

1 Intruduction of ANOVA

1.1 terminology

If we have 4 groupps of samples, with mean ${\mu }_1,{\mu }_2,{\mu }_3,{\mu }_4$, respectively. If we use t-test to test whether the means of 4 population are equle, we have to repeat 6 times t-test.
If all tests are made at some specified significance level (the possibility of error I $\alpha$), the overall level of 6 tests together will be $1-(1-\alpha {)}^6=0.625>>0.05$.

Generally speaking, with the increase of the times of carrying on the significant test, the significant level will decrease.

ANOVA (analysis of variance) is used to test equality of multiple overall mean value.

Suppose we want to compare the quality of different industries according to the number of complaints received.

Here, the object be tested (diferent industries) is defined as factor, and the proformence of the factor(the number of complaints received) is defined as treatment. One-way anova means there are only one factor.

1.2 Principles and basic ideas

1. describe with plot
   Using scatter plot to explore the data, and check the diference.
2. error separation
   SST: Reflecting the error of all datas.
   SSE: Reflecting the with-in group error.
   SSA: Reflecting the group error.
3. error analysis
   Analyse where the error comes from, with-in group or between group.

1.3 Assumption

1. The populations are normal distributions.
2. The populations have the same variance.
3. observation is independent.

Typically:
$$\begin{gathered} H_0:{\mu }_1={\mu }_2=...={\mu }_k \\ {H}_1:{\mu }_i\ne {\mu }_{j}forsomepair(i,j) \end{gathered}$$

Exrcise

Start by installing (if needed) and loading:

• car
• lmtest
• multcomp

One-way anova analysis is used when we want to see if the mean of a continuous variable differs between groups (i.e. between levels of a single categorical variable, a.k.a. factor). It is a generalisation of the t-test, and can be applied to more than two groups. The significance of the categorical variable depends on the relationship between the within-group variance and the among-group variance. If the differences between groups are large compared to the variation within each group, then the categorical variable is likely to be significant. If you are comparing more than two groups, some follow-up analysis (a posthoc test or planned comparison/contrast) is usually necessary to determine exactly which groups differ from each other.

One-way anova with posthoc test

We will start off with an example, an analysis of how Daphnia growth rates depend on what type of parasite individuals are infected with. There were 4 treatments; control and three different species of parasite.

1 Data import and exploration

daphnia = read.csv("daphniagrowth.csv")
boxplot(growth.rate~parasite, data = daphnia)

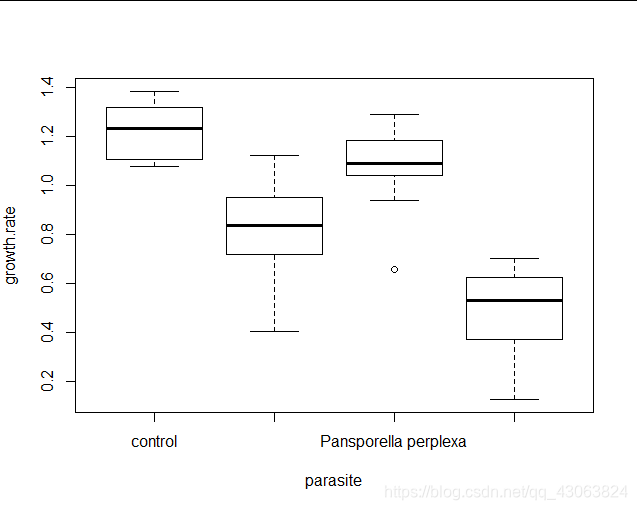
2 Construct one-way anova model

Believe it or not, but a one-way anova is just another type of linear model. R knows that this data should be analysed using a one-way anova because parasiteis a factor. Because of the flexibility of the linear