记录下自己犯得错
- 四元数归一化:
Eigen::Quaterniond q1 = Eigen::Quaterniond (0.1,0.2,0.1,0.3).normalized(); //定义一个四元数并用normalized()归一化
如果把四元数取共轭再归一化,则表示一个相反的旋转。
- 定义一个向量
Eigen::Vector3d p,t;
p << 1.2,0.2,3.2;
t << 1,1,2;
// 定义一个向量并赋值
- 四元数乘法
Eigen::Vector3d p2;
p2=q * p + t; // t 为平移向量
cout << p2 <<endl;
四元数的乘法 四元数应该放在向量前面,基础错误;
附视觉SLAM十四讲题3-7代码:
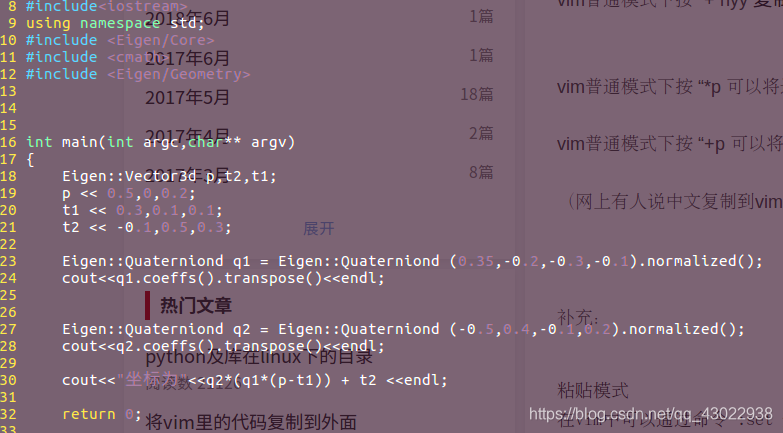





 博客记录了作者在四元数方面所犯的错误,包括四元数取共轭再归一化表示相反旋转,以及四元数乘法时应将四元数放在向量前面这一基础错误,还附上了视觉SLAM十四讲题3 - 7的代码。
博客记录了作者在四元数方面所犯的错误,包括四元数取共轭再归一化表示相反旋转,以及四元数乘法时应将四元数放在向量前面这一基础错误,还附上了视觉SLAM十四讲题3 - 7的代码。
















 1446
1446

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








