本文介绍了二叉搜索树的概念，包括其定义和性质。文章详细阐述了二叉搜索树的节点结构，并讨论了如何进行基本操作，如构造、析构、拷贝和赋值。还提及了二叉搜索树的遍历方法，特别是中序遍历在获取有序序列中的应用。此外，文章详细讲解了二叉搜索树中的数据查找、插入和删除操作，特别强调了删除操作的四种情况及其处理方式。
二叉搜索树，也叫做二叉排序树，
可以是一棵空树，或者是具有下列性质的二叉树：
a.若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
b.若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
c.它的左、右子树也分别为二叉排序树。
例如下图就是一棵二叉搜索树，满足?的性质
(我是一条华丽的分割线～～～～～～～～～～～）
二叉树搜索树的节点
作为一棵二叉搜索树来说，它只需要知道根、根的左右孩子、以及所对应的值，就可以完成一些基本操作。而这里构造函数所采用的初始化列表呢，如果不是很懂用法，可以参考我的另一篇博客（https://mp.youkuaiyun.com/mdeditor/86528744#）
template<class T> //类模版
struct BSTreeNode
{
BSTreeNode(const T& key)
: _left(nullptr)
, _right(nullptr)
, _key(key)
{
}
BSTreeNode* _left;
BSTreeNode* _right;
T _key;
};
template<class T>
class BSTree
{
typedef BSTreeNode<T> Node;
public:
BSTree()
:_root(nullptr)
{ }
private:
Node* _root;
};
二叉搜索树的析构函数、拷贝构造函数以及赋值：
//销毁
void Destroy(Node* root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
}
//析构
~BSTree()
{
Destroy(_root);
_root = nullptr;
}
// 相当于前序拷贝
Node* Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* newnode = new Node(root->_key);
//拷贝左子树和右子树，并与根连接起来
newnode->_left = Copy(root->_left);
newnode->_right = Copy(root->_right);
return newnode;
}
//拷贝 copy(t)
BSTree(const BSTree<T>& tree)
{
_root = Copy(tree._root);
}
//赋值
//BSTree <T>& operator=(const BSTree<T>& tree)
//{
// if (this != &tree)
// {
// Destroy(this->_root);
// this->_root = Copy(tree._root);
// }
// return *this;
//}
//t1 = t2;
BSTree<T>& operator=(BSTree<T> tree)
{
swap(_root, tree._root);
return *this;
}
二叉搜索树的基本操作
对于树来说，都可以使用那三种遍历方法(前序、中序、后序遍历)，不是很懂的童鞋，可以参考我之前的博客(https://blog.youkuaiyun.com/qq_42978418/article/details/88233555)笔者知识有限，也欢迎大家帮我纠正错误。
这里我们就简单的实现一下中序遍历 (中序遍历可得到有序的数列哦）
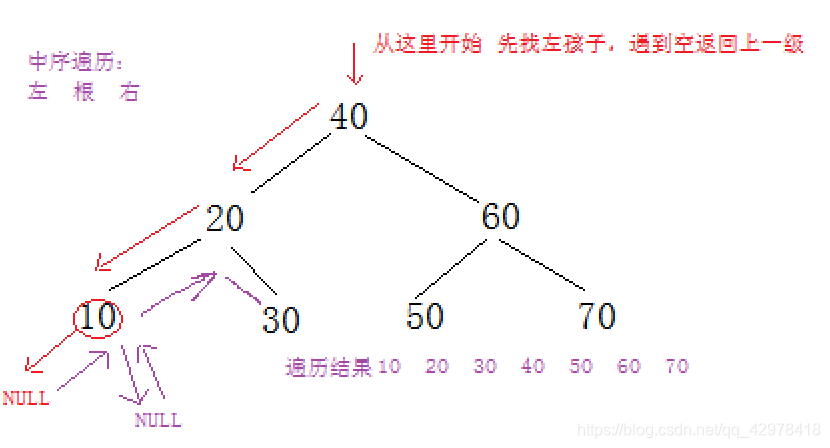
//中序遍历
void _InOrder(Node* root)
{
if (root)
{
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
}
二叉搜索树的数据查找
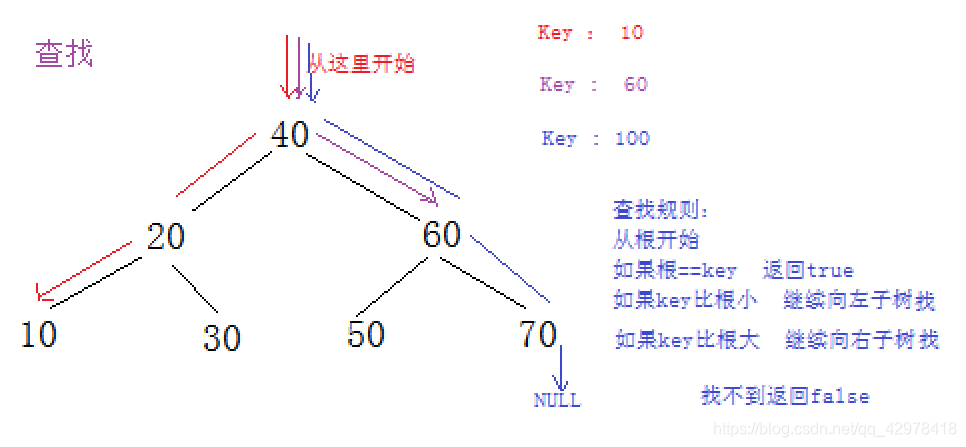
//查找 一般情况下时间复杂度为O(logN)
Node* Find(const T& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key == key)
{
return cur;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
cur = cur->_right;
}
}
return nullptr;
}
二叉搜索树数据的插入
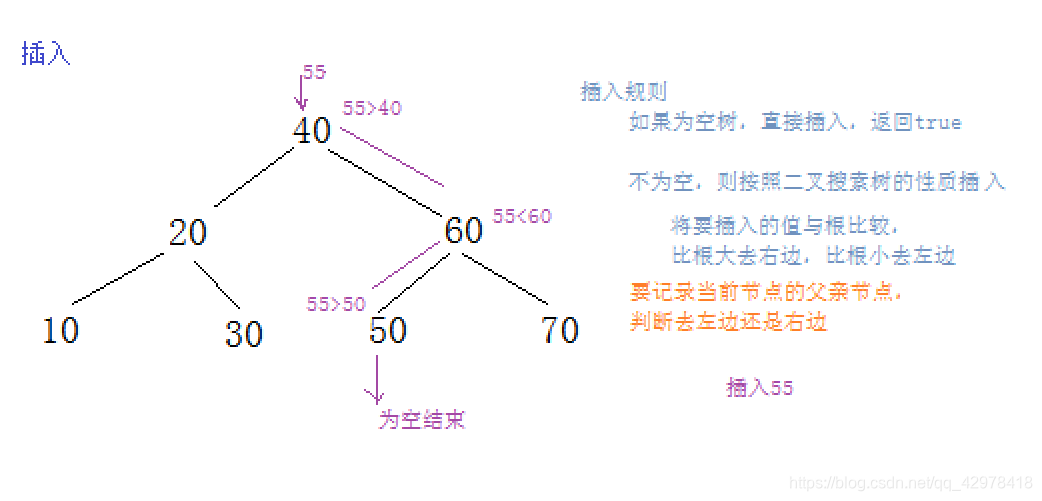
//插入
bool Insert(const T& key)
{
//空树
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
//找插入位置
Node* cur = _root;
Node* Parent = nullptr;
while (cur)
{
Parent = cur;
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return false;
}
}
//插入
cur = new Node(key);
//将cur与上一个节点链起来
if (key < Parent->_key)
Parent->_left = cur;
else
Parent->_right = cur;
return true;
}
二叉搜索树数据的删除
删除大致分为四种情况，要删除的节点没有左孩子、没有右孩子和既有右孩子也没有左孩子，而没有孩子的话，直接将当前节点的父亲指向NULL即可。
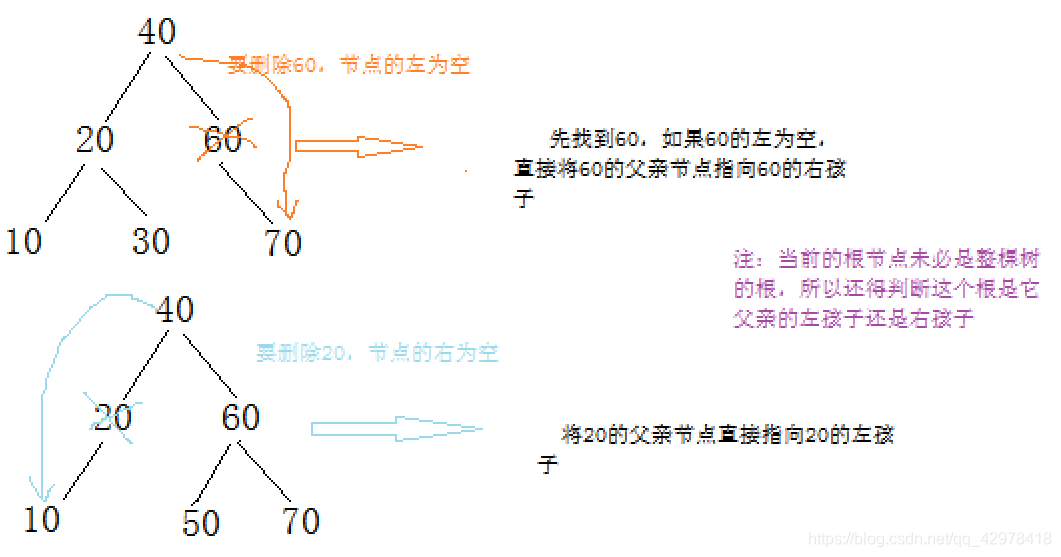
//删除
bool Erase(const T& key)
{
Node* parent = nullptr;
Node* cur = _root;
//如果这棵树为空，则删除失败
if (cur == nullptr)
return false;
//先在树中找到那个date值
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else
{
Node* tmp = cur;
//到这里，cur为要删除的节点，进行删除操作
//cur的左节点为空，父亲指向节点的右，删除节点
if (cur->_left == nullptr)
{
//注意注意 要判断Parent如果为空，则cur->right为新的根节点
if (parent == nullptr)
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
}
//cur的右节点为空，父亲指向节点的左，删除节点
else if (cur->_right == nullptr)
{
//Parent如果为空，则cur->left为新的根节点
if (parent == nullptr)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
}
//cur的左右节点为不为空
//找左树的最左节点 或者 右树的最左节点，交换，删除那个最右或最左节点
else
{
Node* parent = cur;
Node* replace = parent->_left;
while (replace->_right)
{
parent = replace;
replace = replace->_right;
}
//replace为左树的最右节点
cur->_key = replace->_key;
//删除replace
if (replace == parent->_right)
{
parent->_right = replace->_left;
}
else
{
parent->_left = replace->_left;
}
tmp = replace;
}
delete tmp;
return true;
}
}
return false;
}
二叉搜索树的删除很重要，，注意细节。（今天也要加油鸭）
附上源码
#include <iostream>
using namespace std;
template<class T>
struct BSTreeNode
{
BSTreeNode(const T& key)
: _left(nullptr)
, _right(nullptr)
, _key(key)
{
}
BSTreeNode* _left;
BSTreeNode* _right;
T _key;
};
template<class T>
class BSTree
{
typedef BSTreeNode<T> Node;
public:
BSTree()
:_root(nullptr)
{ }
~BSTree()
{
Destroy(_root);
}
//销毁
void Destroy(Node* root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
}
//析构
~BSTree()
{
Destroy(_root);
_root = nullptr;
}
// 相当于前序拷贝
Node* Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* newnode = new Node(root->_key);
//拷贝左子树和右子树，并与根连接起来
newnode->_left = Copy(root->_left);
newnode->_right = Copy(root->_right);
return newnode;
}
//拷贝 copy(t)
BSTree(const BSTree<T>& tree)
{
_root = Copy(tree._root);
}
//赋值
//BSTree <T>& operator=(const BSTree<T>& tree)
//{
// if (this != &tree)
// {
// Destroy(this->_root);
// this->_root = Copy(tree._root);
// }
// return *this;
//}
//t1 = t2;
BSTree<T>& operator=(BSTree<T> tree)
{
swap(_root, tree._root);
return *this;
}
//中序遍历
void _InOrder(Node* root)
{
if (root)
{
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
//查找 一般情况下时间复杂度为O(logN)
Node* Find(const T& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key == key)
{
return cur;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
cur = cur->_right;
}
}
return nullptr;
}
//插入
bool Insert(const T& key)
{
//空树
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
//找插入位置
Node* cur = _root;
Node* Parent = nullptr;
while (cur)
{
Parent = cur;
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return false;
}
}
//插入
cur = new Node(key);
//将cur与上一个节点链起来
if (key < Parent->_key)
Parent->_left = cur;
else
Parent->_right = cur;
return true;
}
//删除
bool Erase(const T& key)
{
Node* parent = nullptr;
Node* cur = _root;
//如果这棵树为空，则删除失败
if (cur == nullptr)
return false;
//先在树中找到那个date值
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else
{
Node* tmp = cur;
//到这里，cur为要删除的节点，进行删除操作
//cur的左节点为空，父亲指向节点的右，删除节点
if (cur->_left == nullptr)
{
//注意注意 要判断Parent如果为空，则cur->right为新的根节点
if (parent == nullptr)
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
}
//cur的右节点为空，父亲指向节点的左，删除节点
else if (cur->_right == nullptr)
{
//Parent如果为空，则cur->left为新的根节点
if (parent == nullptr)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
}
//cur的左右节点为不为空
//找左树的最左节点 或者 右树的最左节点，交换，删除那个最右或最左节点
else
{
Node* parent = cur;
Node* replace = parent->_left;
while (replace->_right)
{
parent = replace;
replace = replace->_right;
}
//replace为左树的最右节点
cur->_key = replace->_key;
//删除replace
if (replace == parent->_right)
{
parent->_right = replace->_left;
}
else
{
parent->_left = replace->_left;
}
tmp = replace;
}
delete tmp;
return true;
}
}
return false;
}
private:
Node* _root;
};
void Test()
{
BSTree<int> t;
//t.Insert(4);
//t.Insert(3);
//t.Insert(2);
//t.Insert(5);
//t.Insert(0);
//t.Insert(3);
//t.Insert(7);
//t.Insert(8);
//t.Insert(5);
//t.Insert(1);
//t.Insert(9);
//t.InOrder();
//t.Erase(7);
//t.InOrder();
int a[] = { 5,3,4,1,7,8,2,6,0,9 };
for (auto e : a)
{
t.Insert(e);
}
t.InOrder();
BSTree<int> copy(t);
t.Erase(2);
t.Erase(8);
t.Erase(1);
t.Erase(5);
t.InOrder();
for (auto e : a)
{
t.Erase(e);
}
t.InOrder();
copy.InOrder();
t = copy;
t.InOrder();
}
int main()
{
Test();
return 0;
}
扫一扫
193
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
