二叉树的建立及应用
二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”和“右子树”。
我们则需要掌握二叉树的一些基本操作和应用,如二叉树的构建、遍历和求节点个树。
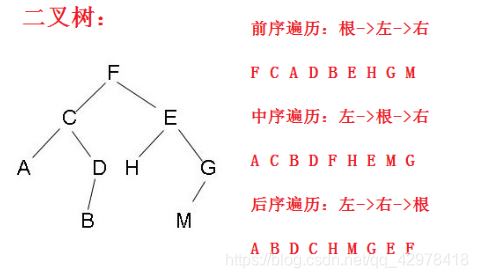
讲这些之前我们先用一棵二叉树来讲解一下什么是前序遍历、中序遍历和后序遍历。
前序遍历指的就是:先访问根节点,再访问该节点的左孩子和右孩子。
中序遍历指的就是:先访问左孩子,再访问根节点,最后访问右孩子;
后序遍历指的就是:先访问左右孩子,最后访问根节点。
1. 构建二叉树
首先我们用前序遍历的数组构建二叉树:
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
if (a[*pi] != '#')
{
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
root->_data = a[*pi];
(*pi)++;
root->_left = BinaryTreeCreate(a, n, pi);
(*pi)++;
root->_right = BinaryTreeCreate(a, n, pi);
return root;
}
else
return NULL;
}
2. 二叉树的遍历
//前序遍历:先访问根节点,再访问该节点的左孩子和右孩子
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
return;
printf("%c ", root->_data);
BinaryTreePrevOrder(root->_left);
BinaryTreePrevOrder(root->_right);
}
//中序遍历:先访问左孩子,再访问根节点,最后访问右孩子
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
return;
BinaryTreeInOrder(root->_left);
printf("%c ", root->_data);
BinaryTreeInOrder(root->_right);
}
//后序遍历:先访问左右孩子,最后访问根节点
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
return;
BinaryTreeInOrder(root->_left);
BinaryTreeInOrder(root->_right);
printf("%c ", root->_data);
}
// 层序遍历:按照树的每一层(高度)进行遍历。
void BinaryTreeLevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root != NULL)
QueuePush(&q, root);
while (QueueEmpty(&q) != 0)
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%c ", front->_data);
if (front->_left != NULL)
QueuePush(&q, front->_left);
if (front->_right != NULL)
QueuePush(&q, front->_right);
}
QueueDestory(&q);
}
3. 二叉树的应用
//求节点个数
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
return 0;
else
return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}
//叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->_left == NULL && root->_right == NULL)
return 1;
return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}
//第K层的个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
if (root == NULL)
return 0;
if (k == 1)
return 1;
return BinaryTreeLevelKSize(root->_left, k - 1)+
BinaryTreeLevelKSize(root->_right ,k-1);
}
//查找X值,返回X节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return NULL;
if (root->_data == x)
return root;
BTNode* ret = BinaryTreeFind(root->_left,x);
if (ret) //ret不为0则为真
return ret;
ret = BinaryTreeFind(root->_right, x);
if (ret)
return ret;
return NULL;
}
//判断一棵树是否为完全二叉树
int BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root != NULL)
QueuePush(&q, root);
while (QueueEmpty(&q) != 0)
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
{
break;
}
QueuePush(&q, front->_left);
QueuePush(&q, front->_right);
}
while (QueueEmpty(&q) != 0)
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front != NULL)
{
return 0;
}
}
return 1;
QueueDestory(&q);
}
以下是笔者的源代码。
BTree.h
#include <stdio.h>
#include <malloc.h>
#include <stdlib.h>
typedef char BTDataType;
typedef struct BinaryTreeNode
{
BTDataType _data;
struct BinaryTreeNode* _left;
struct BinaryTreeNode* _right;
}BTNode;
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
void BinaryTreeDestory(BTNode* root);
int BinaryTreeSize(BTNode* root);
int BinaryTreeLeafSize(BTNode* root);
int BinaryTreeLevelKSize(BTNode* root, int k);
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 遍历
void BinaryTreePrevOrder(BTNode* root);
void BinaryTreeInOrder(BTNode* root);
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
void testTree();
BTree.c
#include "BTree.h"
#include "Queue.h"
#include "Stack.h"
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
if (a[*pi] != '#')
{
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
root->_data = a[*pi];
(*pi)++;
root->_left = BinaryTreeCreate(a, n, pi);
(*pi)++;
root->_right = BinaryTreeCreate(a, n, pi);
return root;
}
else
return NULL;
}
//销毁
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL)
return;
else
{
BinaryTreeDestory(root->_left);
BinaryTreeDestory(root->_right);
free(root);
}
root = NULL;
}
//结点个数
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
return 0;
else
return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}
//叶子结点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->_left == NULL && root->_right == NULL)
return 1;
return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}
//第K层的个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
if (root == NULL)
return 0;
if (k == 1)
return 1;
return BinaryTreeLevelKSize(root->_left, k - 1)+
BinaryTreeLevelKSize(root->_right ,k-1);
}
//查找X值,返回X结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return NULL;
if (root->_data == x)
return root;
BTNode* ret = BinaryTreeFind(root->_left,x);
if (ret) //ret不为0则为真
return ret;
ret = BinaryTreeFind(root->_right, x);
if (ret)
return ret;
return NULL;
}
//前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
return;
printf("%c ", root->_data);
BinaryTreePrevOrder(root->_left);
BinaryTreePrevOrder(root->_right);
}
//中序遍历
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
return;
BinaryTreeInOrder(root->_left);
printf("%c ", root->_data);
BinaryTreeInOrder(root->_right);
}
//后序遍历
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
return;
BinaryTreeInOrder(root->_left);
BinaryTreeInOrder(root->_right);
printf("%c ", root->_data);
}
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root != NULL)
QueuePush(&q, root);
while (QueueEmpty(&q) != 0)
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%c ", front->_data);
if (front->_left != NULL)
QueuePush(&q, front->_left);
if (front->_right != NULL)
QueuePush(&q, front->_right);
}
QueueDestory(&q);
}
//判断一棵树是否为完全二叉树
int BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root != NULL)
QueuePush(&q, root);
while (QueueEmpty(&q) != 0)
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
{
break;
}
QueuePush(&q, front->_left);
QueuePush(&q, front->_right);
}
while (QueueEmpty(&q) != 0)
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front != NULL)
{
return 0;
}
}
return 1;
QueueDestory(&q);
}
Queue.h
#include <stdio.h>
#include <assert.h>
#include <malloc.h>
#include <stdlib.h>
#include "BTree.h"
typedef BTNode* ElemType;//定义数据类型
typedef struct sqQueue
{
ElemType _data;
struct sqQueue* _next;
}sqQueue;
typedef struct Queue
{
sqQueue* _front;
sqQueue* _tail;
}Queue;
void QueueInit(Queue *q);
void QueueDestory(Queue *q);
int QueueEmpty(Queue *q);
void QueuePush(Queue *q, ElemType x);
void QueuePop(Queue *q);
ElemType QueueFront(Queue *q);
Queue.c
#include "Queue.h"
//初始化
void QueueInit(Queue *q)
{
assert(q);
q->_front = q->_tail = NULL;
}
//销毁
void QueueDestory(Queue *q)
{
assert(q);
sqQueue* cur = q->_front;
while (cur)
{
sqQueue* next = cur->_next;
free(cur);
cur = next;
}
q->_front = q->_tail = NULL;
}
//判断队列是否为空,0为空,1不为空
int QueueEmpty(Queue *q)
{
return q->_front == NULL ? 0 : 1;
}
//入队
void QueuePush(Queue *q, ElemType x)
{
assert(q);
sqQueue* node = (sqQueue *)malloc(sizeof(sqQueue));
node->_data = x;
node->_next = NULL;
if (q->_tail == NULL)
{
q->_tail = q->_front = node;
}
else
{
q->_tail->_next = node;
q->_tail = node;
}
}
//出队
void QueuePop(Queue *q)
{
assert(q);
sqQueue* front = q->_front->_next;
free(q->_front);
q->_front = front;
if (front == NULL)
q->_tail = NULL;
}
//出队头元素
ElemType QueueFront(Queue *q)
{
assert(q);
ElemType tmp = q->_front->_data;
return tmp;
}
////打印
//void Queueprint(Queue *q)
//{
// sqQueue *tmp = q->_front;
// while (tmp)
// {
// printf("%d ", tmp->_data);
// tmp = tmp->_next;
// }
// printf("\n");
//}
test.c
#include "BTree.h"
#include "Queue.h"
void testTree()
{
char arr[] = "ABD##E#H##CF##G##";
int sz = sizeof(arr) / sizeof(arr[0]);
int i = 0;
BTNode* b = BinaryTreeCreate(arr, sz, &i);
printf("遍历:\n");
BinaryTreePrevOrder(b);
printf("\n");
BinaryTreeInOrder(b);
printf("\n");
BinaryTreePostOrder(b);
printf("\n");
printf("结点个数: ");
int num = BinaryTreeSize(b);
printf("%d\n", num);
printf("叶子结点个数: ");
int n = BinaryTreeLeafSize(b);
printf("%d\n", n);
printf("第K层结点个数: ");
int m = BinaryTreeLevelKSize(b, 4);
printf("%d\n", m);
BTNode* ret = BinaryTreeFind(b, 'C');
printf("%c\n", ret->_data);
BinaryTreeLevelOrder(b);
printf("\n");
printf("是否为完全二叉树(是为1,否为0): ");
printf("%d\n", BinaryTreeComplete(b));
printf("\n");
BinaryTreeDestory(b);
}
int main()
{
testTree();
return 0;
}





















 769
769

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








