【论文阅读】Remote Sensing Image Super-Resolution Using Sparse Representation and Coupled Sparse Autoencod

论文地址

1、论文地址

摘要：

遥感图像超分辨率（SR）是指提高空间分辨率的技术，有利于后续的图像解译，如目标识别、分类和变化检测。在流行的基于稀疏表示的方法中，由于复杂的成像条件和未知的退化过程，低分辨率（LR）观测图像的稀疏系数很难与真实的高分辨率（HR）对应物一致，这导致不能令人满意的 SR结果。

为了解决这个问题，本文提出了一种新颖的耦合稀疏自动编码器（CSAE），以有效地学习 LR 和 HR 图像之间的映射关系。具体来说，首先将LR和HR图像用一组稀疏系数表示，然后建立CSAE来学习它们之间的映射关系。
由于所提出的方法利用了稀疏分解和CSAE的特征表示能力，可以准确地获得LR和HR图像之间的映射关系。在实验上，在三个具有不同空间分辨率的真实世界遥感图像数据集上，将所提出的方法与几种最先进的图像 SR 方法进行了比较。广泛的实验结果表明，所提出的方法在所有三个数据集的平均峰值信噪比和结构相似性测量方面都取得了实质性的改进。此外，结果还表明，随着放大因子的增加，所提出的方法比其他竞争方法具有更突出的性能。

I. 简介

在过去的几十年里，具有米或亚米空间分辨率的遥感图像已经公开可用。尽管最近有了这样的发展，但它的空间分辨率不能满足生产和应用对图像日益增长的需求。这已经严重阻碍了遥感技术的进一步发展和应用，而提高传感器的分辨率成本和难度都相当大。然而，图像超分辨率（SR）技术提供了一种低成本且有效的方法来缓解这个问题。图像 SR 可以突破传感器本能分辨率的限制和大气的影响 [1], [2], 可以产生质量更好、分辨率更高的图像, 为进一步的图像分析和应用提供基础 [3] ].在过去的几十年里，一系列的图像SR方法被提出，大致可以分为三类[4]：
1）基于插值的方法；
2）基于重建的方法；
3) 基于学习的方法。
基于插值的方法是最直观的方法，它使用线性、双线性或双三次插值获取高分辨率 (HR) 图像。然而，插值操作总是不可避免地使图像模糊，基于重建的方法包括迭代反投影[5]、凸集投影（POCS）[6]、最大后验概率（MAP）和正则化方法。张等。 [7] 使用 POCS 重建三视图遥感图像。罗等。 [8]修改了MAP和变量贝叶斯方法来恢复遥感图像，虽然计算量大，但取得了相当满意的结果。正则化方法 [9] 通过引入全变正则化项将原始不适定问题转换为优化问题。基于重建的方法[10]的优点是一些局部先验假设足以缓解插值引起的模糊现象。但是，当upscaling factor比较大时，不容易获得准确的子像素运动信息，对重建结果有很大的影响。因此，结合不同重建方法优点的混合方法也得到了广泛的应用。然而，由于重建方法重建亚像素运动信息的能力较差，混合方法不能满足重建精度。
基于学习的图像 SR 方法旨在通过机器学习方法挖掘低分辨率 (LR) 与相应的 HR 图像块之间的关系。它们主要包括基于马尔可夫网络的方法、邻域嵌入方法、基于深度学习的方法和基于稀疏表示的方法。基于马尔可夫网络的方法[11]、[12]基于给定的 LR 图像为 HR 图像构建概率场，然后通过最大化条件概率重建 HR 图像。邻域嵌入方法起源于流形学习，它假设在 LR 和 HR 图像的特征空间中存在一些相似的几何结构。因此，相应的 HR 图像是通过约束中心块与其邻域之间的平滑度来预测的 [13]。基于深度学习的方法 [14]-[19] 在 HR 训练样本的监督下提取具有深层网络隐藏层的图像特征。受益于深层网络结构，深度学习方法可以为 SR 捕获图像的信息特征。然而，为了有效地捕获所需的图像特征，它们总是需要大量的训练样本和计算资源。实际上，图像信号可以表示为局部范围内冗余字典中一系列基本结构元素的线性组合[ 20], [21]。基于此，稀疏表示 [22] 旨在将 LR 和 HR 图像块分解为相应冗余字典上的稀疏系数。通过使用联合字典训练策略[20]，LR 和 HR 图像的稀疏系数被约束为一致。然后，可以使用LR稀疏系数根据训练好的HR字典重建相应的HR图像。由于它们有前途的性能，已经提出了许多修改后的变体 [23]-[26] 来适应各种任务。他等人。 [27] 用 beta 过程训练联合字典，可以去除冗余字典中的一些无用元素。他们没有将 LR 和 HR 图像的稀疏系数约束为相等，而是建立了一个权重矩阵来将 LR 系数映射到 HR 系数。 Peleg 和 Elad [28] 利用统计模型来约束 LR 和 HR 系数之间的映射，然后通过最小化最优问题来求解字典。此外，还使用级联策略来提高重建精度。叶干利等。 [29] 和张等人。 [30] 训练了更具特色的目标字典，例如边缘、梯度和结构，以便可以选择相应的字典来为特定类型的图像产生更好的重建结果。一般来说，大多数现有的基于稀疏表示的图像 SR 方法[31]-[34]使用联合词典训练策略或其变体来训练词典，其LR系数可以直接用作HR系数或者可以构建权重矩阵来桥接它们。然而，由于复杂的成像条件和未知的退化过程，不同空间尺度（或分辨率）的遥感图像所包含的信息通常差异很大（即使是同一场景）。因此，不同空间尺度的图像具有不同的优化稀疏表示。使用简单线性映射的训练策略很难体现它们复杂的对应关系，这已成为进一步图像 SR 的重要限制。在本文中，我们提出了一种新颖的耦合稀疏自动编码器 (CSAE)，利用学习策略挖掘 LR 和 HR 稀疏系数之间的映射关系。同时，由于 CSAE 接受稀疏系数作为先验知识来指导学习过程，所提出的方法利用了稀疏分解和 CSAE 的特征表示能力。因此，可以从给定的LR稀疏系数中准确估计出HR系数，并用于HR图像重建。三个遥感图像数据集的实验结果表明，所提出的方法在不同的空间分辨率下取得了令人印象深刻的重建结果。此外，与联合字典训练方法相比，该方法预测的HR系数也表现出与真实值更大的相关性。第二部分介绍了图像 SR 的初步设置和问题设置。第三节描述了所提出方法的细节。实验结果和进一步的讨论随后在第四节中介绍。最后，在第五节中对我们的工作进行了总结和对未来工作的布局。

二。初步和问题设置

观察到的图像可以看作是通过一系列退化过程从 HR 图像获得的 LR 图像，包括光学调光、子采样和加性噪声。我们的目标是根据观察到的 LR 图像重建相应的 HR 图像。令 Ih 和 Il 分别为 HR 图像和 LR 图像。退化模型通常可以表示如下：

其中 S 表示下采样矩阵，B 表示模糊矩阵，n ̃ 是加性噪声。从观察到的 LR 图像重建 HR 图像，关键是建立它们之间的映射关系。然而，由于未知的退化因素，这在实践中是一项非常困难的任务，而 LR 和 HR 图像都可以通过局部范围内相应冗余字典的稀疏系数线性表示。因此，可以在 LR 图像和 HR 图像的稀疏系数之间交替建立关系。对于给定的 LR 图像块 pl（从 LR 图像中提取并已展平为向量），它可以表示为乘积冗余字典和对应的稀疏系数

其中Dl是LR图像的冗余字典，αl是LR图像(SCOLRI)对应的稀疏系数，其大部分元素为零。类似地，HR 图像块 ph 也可以表示为 ph ≈ Dhαh。稀疏系数 αl 和 αh 可以分别视为 pl 和 ph 的特征，αl 和 αh 之间的关系暗示了 LR 和 HR 图像之间的关系。

字典训练的常规方法是联合字典训练策略[20]，它通过解决以下优化问题来一起训练 LR 和 HR 字典：

其中D = [Dh] 和 p = [ph]。 ∥ ∥0 表示 l0 范数，Dl plλ 是稀疏约束的惩罚因子。联合字典训练策略通过将 LR 和 HR 图像块堆叠在一起来训练字典，使得 LR 块 pl 和 HR 块 ph 被约束在其对应的字典上共享相同的稀疏系数。在图像SR处理过程中，给定的LR图像块pl在LR字典Dl上进行分解，得到稀疏系数α。然后通过稀疏系数 α 与 HR 字典 Dh 的线性组合预测 HR 图像块，即 ph = Dhα。最后，通过将预测的 HR 图像块拼接在一起来重建 HR 图像。
然而，由于LR和HR图像具有不同的频率范围，它们实际上需要不同数量的基本结构单元来进行稀疏表示。联合字典训练策略将LR和HR图像的稀疏系数限制为具有相同的长度，这使得LR和HR图像的字典很难最佳地表示其图像空间。为了解决这个问题，He等人[27]用beta过程训练了字典，该过程利用权重矩阵来反映LR和HR系数之间的映射。无论如何，无论是强制LR和HR图像的稀疏系数相等，还是假设存在线性映射关系，都不足以表征真实的复杂图像SR过程。因此，本文旨在建立一种新的CSAE来准确学习LR和HR稀疏系数之间的映射。值得注意的是，根据（1），我们有以下等式：

其中 S -1 是矩阵 S 的逆（或伪逆），称为插值矩阵。 I ̃ = BI 表示LR图像，lhi是从HR图像Ih模糊或者从LR图像I上采样得到的。 .令 H = I − B，我们有 Ihl = HIh，H 是高通矩阵。因此，残差（HR图像和上采样的LR图像之间的差异）包含了原始HR图像的高频成分，例如纹理、边缘等（见图1）。HR图像具有与LR图像相同的低频信息，我们只需要估计它们的残差Ihl。然后可以通过将估计的残差添加到上采样的 LR 图像来重建 HR 图像，即 Ih = I + I ̃。

三. 稀疏分解的SR与CSAE

本文提出了一种新的CSAE来学习LR图像稀疏系数与CSAE之间的映射关系残差。训练完成后，可以通过提出的 CSAE 预测残差的稀疏系数（SCOR），然后可以进一步估计残差。最后，通过将估计的残差添加到上采样的 LR 图像（见图 2）来重建最终的 HR 图像。

图 2.所提出的图像超分辨率方法框架.
在训练阶段，LR 图像和残差（HR 和上采样 LR 图像之间的差异）表示为稀疏系数，并且训练 CSAE 以了解它们的映射关系。
在测试阶段，我们首先将给定的LR图像表示为稀疏系数，并使用学习的CSAE预测残差的稀疏系数。
然后根据其预测的稀疏系数估计残差，并通过将估计的残差添加到上采样的LR图像中来重建最终的HR图像。

A. Image Sparse Decomposition

本节将介绍如何将LR图像的patches和残差分解为稀疏系数。表示LR图像块为Pl =[p(1),p(2),…]，LR图像Dl对应的ll冗余字典可以用如下优化问题训练：

其中 αl 表示相应的 SCOLRI。这是一个具有 l0 范数约束的 NP-hard 问题，需要一个贪心算法来逼近近似解。尽管如此，Donoho [35] 已经表明，当字典足够冗余时，这个 l0 范数问题等同于以下 l1 范数问题：

其中 λs 是稀疏约束的惩罚因子。字典 Dl 可以使用 K-SVD [36] 算法通过丰富的图像样本进行训练，并且可以同时求解相应的稀疏系数 αl。类似地，残差的补丁 Phl = [p(1) , p(2) , p(2) , . . .] hl hl也可以用优化问题分解如下：

其中αhl是残差的稀疏系数，Dhl是对应的字典。 αhl 和 Dhl 通过使用 K-SVD 算法最小化（7）来求解。
之后，LR 图像的分解稀疏系数和残差（即 αl 和 αhl）被用作所提出的 CSAE 的训练样本（参见第 III-B).

B. Mapping Learning With CSAE

Image SR是恢复LR图像的高频分量，相当于从给定的SCOLRI αl ∈ Rdl中估计出SCOR αhl ∈ Rdhl。为此，许多相关方法已经提出 [27]-[30]。然而，它们大多是线性映射，不能准确反映低频和高频之间的关系。此外，由于离散采样和噪声，线性映射难以表征图像SR的内部机制。

针对这些问题，本文提出了一种旨在学习αl和αhl之间映射关系的CSAE。具体来说，CSAE 将 αl 和 αhl 映射到一个隐藏的特征空间，在那里它们被限制为相等。因此，我们找到一个过渡特征空间，其中 αl 和 αhl 的隐藏表示彼此相等。将 SCOLRI 映射到它在特征空间中的隐藏表示，然后可以从中重建 SCOR。此外，为了保证重建结果的稀疏性，在映射的每个阶段都需要稀疏约束。

对于给定的SCOLRI αl ∈ Rdl，其隐藏特征表示是通过使用稀疏自编码器（SAE）获得的。SAE是一种神经网络，由隐藏层组成，约束输出等于输入。它由两部分组成：编码器和解码器。编码器将输入 αl 映射到隐藏的特征表示 α（h） l ∈ Rh，而解码器从 α（h） l 重建 αl。将重建的 αl 表示为 αˆl，αˆl 应等于 αl。

从技术上讲，将编码器和解码器表示为 αl 的编码和解码函数。

重建的αl可以表述为

训练 SAE（包括编码器和解码器）的损失函数为

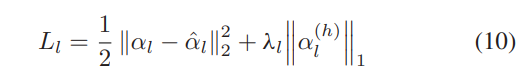
其中 λl 表示稀疏性约束因子，以保持输出结果的稀疏性。一方面，我们约束彼此接近的 αl 和 αˆl。另一方面，隐藏特征 α（h）l 也有望保持稀疏性为 αl。

类似地，我们也可以为 αhl 建立相应的编码器和解码器，满足

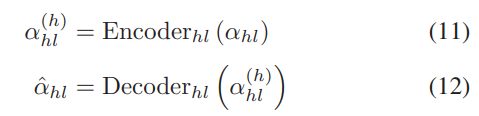
其中α（h） hl ∈ Rh是αhl的隐藏特征，αˆhl表示αhl的重建。相应的损失函数可以表述为

其中 λhl 表示稀疏性约束系数。隐藏表示α（h） l 和 α（h） hl 分别可以看作是 αl 和 αhl 的特征向量。
拟议的CSAE旨在将αl和αhl的SAE耦合在一起，以便可以建立αl和αhl之间的映射关系。
具体来说，CSAE约束它们在特征空间中的隐藏表示相等，即α（h）l = α（h） hl。

因此，所提出的CSAE的损失函数可以表示如下：

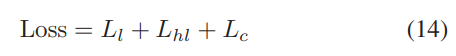
其中

表示耦合损耗，它约束隐藏表示α（h） l和α（h） hl相等。

通过使用随动量的批量随机梯度下降最小化损失函数 （14） 来优化 CSAE 的参数。
一旦模型被训练，我们就有了 α（h） l ≈ α（h） hl ，并且不需要 αl 的解码函数和 αhl 的编码函数（见图 3）。然后可以使用经过训练的编码器和解码器建立 αl 和 αhl 之间的映射关系。
对于给定的SCOLRI αl，相应的估计SCOR可以表述为：

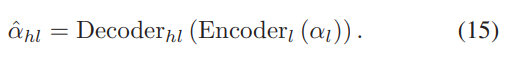
输出 αˆhl 表示 αhl 的重建。方程（15）描述了SCOLRI αl对SCOR αhl的重建过程，反映了LR图像和HR图像之间的映射关系。值得注意的是，αl和αhl的编码器和解码器可以使用任何可微分架构来实现。在本文中，使用了一个隐藏层的神经网络，因为它已经具有挪用任何非线性函数的能力。

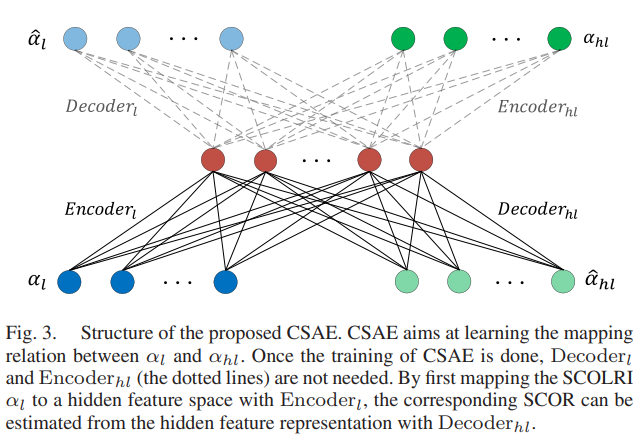
（图3：拟议CSAE的结构。CSAE旨在学习αl和αhl之间的映射关系。一旦完成了CSAE的训练，就不需要解码器和编码器（虚线）。通过首先使用编码器l将SCOLRIαl映射到隐藏特征空间，可以使用解码器l从隐藏特征表示中估计相应的SCOR。）

C. HR Image Reconstruction

本节介绍如何使用稀疏分解和提出的CSAE从给定的LR图像重建HR图像（参见流程1）。对于给定的LR图像Il，我们首先将其切成重叠的补丁Pl = {p（1）l ， p（2）l ,…}。对于每个LR图像面块p（k）l∈Pl，其稀疏系数α（k）l通过求解以下优化问题计算：

其中 Dl 是通过最小化 （6） 求解的 LR 图像字典。

然后，使用拟议的CSAE作为

相应的残差由下式获得

其中 Dhl 是通过最小化 （7） 求解的残差字典。

之后，通过将估计的残差添加到上采样的LR图像中来重建相应的HR图像补丁p（k）h，即

最后，通过将重建的HR图像斑块拼接在一起并平均其重叠度来获得HR图像ˆIh。
值得注意的是，由于噪声的推断，重建的HR图像ˆIh可能不完全满足约束条件。为了消除模糊性，通过以下全局优化问题对最终的HR图像Ih进行优化：

其中μ是正则化项的因素。结果表明，经过模糊和子采样后的最终HR图像应尽可能接近观察到的LR图像。

四、实验结果与讨论

A.实验数据集和设置

为验证所提方法的有效性，应用了3组不同空间分辨率的遥感影像进行实验。它们是具有 1 m 空间分辨率的 NWPU VHR-10 [37] 图像集、具有 5.6 m 空间分辨率的 ZY-3 图像和具有 18 m 空间分辨率的 MOMs-2P 图像。每个图像集分为训练集和测试集，分别占90%和10%。对于每个图像集，测试图像是从测试集中随机选择的。方便的是，五个随机选择的NWPU VHR-10 [37]图像表示为Im1，Im2，…，Im5，五个ZY-3图像表示为Im6，Im7，…，Im10，五个MOM-2P图像表示为Im11，Im12，…，Im15。实验结果采用峰值信噪比（PSNR）和结构相似性（SSIM）两个常用指标进行定量评价。为了便于精度评估，将每个图像集的原始im-age Ih视为HR图像。LRimage I ̃ 由下采样运算符从 I 生成，然后使用双三次算法在给定的比例因子下插值回与 Ih 具有相同的大小。残差 Ihl 的计算公式为 I = I − I ̃ 。一阶和二阶导数用作训练特征，而不是LR图像本身。根据Yang等人[20]的说法，梯度算子用于本文得到LR图像的一阶和二阶导数。通过将这四个梯度算子分别应用于 LR 图像，我们获得每个图像的四个导数并将它们组合在一起作为训练样本。之后，从训练集中随机选择 100000 个大小为 7 × 7 像素的图像块用于字典 train-工程。字典使用 λs = 0.15 的 K-SVD 算法进行训练（参见第 III-A 节）。由于残差仅包含 HR 图像的一小部分信息，因此 LR 和残差的字典大小分别设置为 256 和 64。残差的计算也减少了预测空间和难度。值得注意的是，所提出的方法旨在从具有一个通道的单个图像重建 HR 图像。对于 RGB 彩色图像，我们首先将其转换为 YUV 颜色空间，并且只在 Y 通道重建 HR 图像。然后通过将结果转换回 RGB 颜色空间来获得最终的 HR 图像。此外，为了进一步探索不同放大因子的影响，我们在保持其他实验设置不变的情况下进行了两组比例因子 s = 2 和 s = 3 的实验。在CSAE的训练阶段，神经元数隐藏层设置为192，稀疏约束因子为λl = λhl = 0.1。 (14) 中的损失函数使用批量大小为 100 的随机批量梯度下降算法进行了优化。此外，为了深入理解我们的 CSAE，还分别进一步讨论和分析了几个关键组件的性能。

与其他方法的比较

我们将我们的 SR 结果与其他最先进的图像 SR 方法进行了比较，包括使用冗余字典的压缩感知 (CSRD) [26]、β 过程联合字典学习 (BPJDL) [27]、稀疏结构流形embedding (SSME) [24], and FSRCNN [38].1) Experiments on the NWPU VHR-10 Image Set：The experimental results on the NWPU VHR-10 image set with scale表 I 和表 II 分别提供了因子 s = 2 和 s = 3。结果表明，所提出的方法在大多数测试图像上实现了最高的 PSNR 和 SSIM 测量。此外，放大因子越大，高频信息丢失越多，导致LR和HR图像之间的映射关系越难构建。图 4 和图 5 显示了一些使用所提出的和其他竞争图像 SR 方法重建的 NWPU VHR-10 图像。可以看出，所提出的方法可以很好地保持图像结构和细节。通过将稀疏表示与 CSAE 相结合，所提出的方法可以更准确地挖掘 LR 图像的稀疏系数与残差之间的映射关系，并很好地保留结构和纹理信息。2）在 ZY-3 图像集上的实验： 表III 和 IV 分别显示了比例因子 s = 2 和 s = 3 的 ZY-3 图像的实验结果。总的来说，我们的性能在大多数测试图像上与其他竞争方法相当或更好。此外，与上的结果相比NWPU VHR-10图像集，ZY-3图像的空间分辨率较低，LR与原始HR图像的关系相对简单，重建效果较好。与 NWPU VHR-10 图像相比，对于比例因子 s = 2 和 s = 3，所提出的方法与 MOM-2P 图像的平均 PSNR 分别增加了 8.632 dB 和 5.639 dB。图 6 和图 7 提供了一些用所提出的方法和其他竞争图像 SR 方法重建的 ZY-3 图像。与 NWPU VHR-10 图像集上的实验结果相似，所提出的方法清楚地重建了图像的结构和纹理细节。3) ExperimentontheMOMs-2PImageSet：MOM-2P 图像上的实验结果在表 V 和表 VI 中提供.表 V 中的结果表明，所提出的方法平均实现了最高的 PSNR 和 SSIM 测量，表 VI 提供了与表 V 相似但更好的结果。同时，与在西北工业大学VHR-10和ZY-3图像集上的实验类似，当比例因子变大时，使用所提出的方法在MOM-2P图像上的实验也比其他竞争方法获得了更好的结果。与具有相同放大因子的表 IV 相比，表 VI 中的结果得到了显着改善。
这表明空间分辨率较低的图像由于高频信息较少，因此更容易重建。在图8和图9中，我们展示了一些重建的MOM-2P，分别是s = 2和s = 3。结果表明，所提方法还重建了边缘清晰、细节清晰的HR图像。此外，随着升频因子的增大，LR和HR图像之间的映射变得更加复杂，而所提出的方法相对于其他比较方法变得更加突出。结果表明，所提方法在稀疏域中与CSAE的学习映射关系受益匪浅。

重构信息分析

本节对重构信息进行了进一步的可视化和分析。为此，我们首先可视化字典用稀疏分解训练（见第 III-A 节）。然而，由于冗余字典的每个元素都是一个一维向量，我们将它们重新整形为小的图像块以具有轻松的视觉效果。在不失一般性的情况下，ZY-3 图像的分解字典如图 10 所示。它表明冗余字典反映了图像的结构和纹理特征。此外，直接观察所提出方法的重建信息，我们还在图 11 中可视化了重建的残差及其基本事实（缩放以获得更好的视觉效果）。与图10中的冗余字典类似，图11中的重构残差也是结构和纹理等高频部分。它们恰到好处地补充了 LR 图像缺失的高频信息。与ground truth相比，大部分高频信息已经被重构，并且像素已经根据其相邻像素进行了精确重构。

D. 参数敏感性分析

在本节中，我们进行了更多的实验来分析所提出方法的参数敏感性，主要包括CSAE的隐藏层数和神经元数以及模型训练的稀疏约束因素。我们在比例因子 s = 3.1 的 ZY-3 图像上实现了这些实验）隐藏层分析：在上述实验中，所提出的 CSAE 模型中仅应用了一个隐藏层，CSAE 的隐藏神经元数量设置为192。为方便起见，我们将CSAE的架构表示为256-192-64，其中256和64分别是输入和输出维度。根据第 III-B 节中的模型参数设置，我们进行了两组实验来探索所提出的 CSAE 的隐藏层数和神经元数。每个实验都进行了十倍交叉验证，平均验证误差如图所示12. 在实验(a)中，通过比较神经元编号为256-96-64、256-128-64、256-192-64、256-224-64的验证结果，可以看出最终的评估误差随着隐藏层神经元数量的增加而变低。相比之下，256-192-64 和 256-224-64 表现出相似的性能，但增加了计算成本。在实验 (b) 中，我们增加了 CSAE 的隐藏层数不同的神经元数。我们可以看到，更多的隐藏层不会导致评估误差显着降低，同时可以提高计算复杂度。事实上，一个至少有一个隐藏层的神经网络已经被证明具有逼近任意连续函数的能力，这也为我们的CSAE将映射关系逼近到任意精度提供了保证。2）稀疏约束的敏感性：我们提供了更多的实验来探索稀疏约束因子 λl 和 λhl 的影响，它们分别鼓励重建的 SCOLRI 和 SCOR 的稀疏性。由于 λl 和 λhl 具有相同的数量级，为方便起见，我们让 λl 和 λhl 与 λ 具有相同的值，即 λl = λhl = λ。具体来说，我们在 CSAE 中应用了一系列稀疏约束因子，并通过十倍交叉验证报告了它们的平均性能（见图 13）。实验结果表明，当 λ = 0.1 时，最终验证误差趋于最小。此外，为了直接探索稀疏性约束对重建结果的影响，我们进一步报告了重建图像在三个数据集上的平均 PSNR（见表七).实验结果表明，稀疏约束因子的取值过大和过小都不利于高质量的图像SR。在没有稀疏约束（即λ=0）的情况下，由于模型过拟合，测试PSNR相对较小，而大的稀疏约束（即λ=5.0）也限制了模型的表示能力。

E. 系数之间相关性的讨论

为了进一步证实所提出方法的效率，计算了预测的 SCOR 与地面实况之间的相关系数，并与联合字典训练方法 [20] 进行了比较。预测的SCOR与ground truth的相关系数反映了重构特征信息的一致性。相关性越大表示重建结果越好，反之亦然。为了进行比较，通过分解其冗余字典上的残差来生成相应的基本事实，然后我们分别用所提出的方法和联合字典训练方法对其进行估计。之后，计算并比较真实值与预测结果之间的相关系数。图 14 显示了预测的 SCOR 和真实值之间的相关系数。一般来说，所提出的方法在每个实验中都获得了相对较大的相关系数。该方法的平均相关系数达到0.494，而联合字典训练方法仅为0.306，这意味着该方法更可能反映LR图像的稀疏系数与残差之间的映射关系。此外，随着放大因子的增加，相关系数越来越小。放大因子越大，丢失的高频信息越多，LR图像的稀疏系数与残差之间的映射关系越难构建。此外，随着放大因子的增加，所提出的方法与联合词典训练方法之间的相关性差距越来越大。这意味着我们的方法在 SR 任务的放大因子更大的情况下显示出远远优于传统方法。

鲁棒性测试

在本节中，我们进一步比较了所提出的方法与 FSRCNN [38] 对随机高斯噪声的鲁棒性。具体来说，我们在资源三号图像集上进行了鲁棒性测试实验。 LR图像是通过Bicubic算法对原始图像进行下采样得到的，原始图像被认为是ground truth HR图像。在 SR 阶段，我们将具有一系列方差的随机高斯噪声添加到测试 LR 图像中，以探索所提出的 CSAE 和 FSRCNN [38] 的抗噪声能力。测试结果如图 15 所示。可以看出，与 FSRCNN 相比，所提出的方法对噪声更加稳健。事实上，FSRCNN 倾向于通过应用多层卷积运算符来预测 HR 图像。然而，卷积核无法从输入的 LR 图像中区分噪声，而是将它们视为最终 HR 图像预测的图像信息。相比之下，所提出的方法旨在结合冗余字典中的基本结构和纹理元素来重建 HR 图像。因此，所提出的方法对噪声具有更强的鲁棒性，并且能很好地保持物体的边缘。

五．结论

提出了一种新的 CSAE 来有效地学习图像 SR 的 LR 和 HR 图像之间的映射关系。从技术上讲，我们首先将 LR 和 HR 图像分解为稀疏系数，然后建立 CSAE 来学习它们之间的映射关系。该方法利用了稀疏分解和 CSAE 的特征表示能力，能够学习 LR 和 HR 图像之间的映射关系。在三个不同分辨率的遥感图像数据集上的实验结果表明，所提出的方法获得了可观的收益在视觉效果和量化指标上均优于其他竞争方法。此外，在更大的放大因子下，所提出的方法变得更有前途。在我们的工作中没有考虑针对特定信息（如边缘、纹理和结构）的字典训练。将来，我们会将它们合并到建议的框架中以重建更逼真的图像轮廓。