统计描述

一、统计描述
- 表格法与图形法
- 数值方法
二、表格法与图形法

三、数值方法

四、重点
1.辛普森悖论：从两个或多个单独的交叉分组表得到的结论与一个综合的交叉分组表数据得到的结论可能截然相反。
2.百分位数：提供了数据如何是散布在从最小值与最大值的区间上的信息。
第p百分位数位置

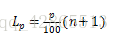
3.四分位数：将数据划为四部分，每一部分大约包含1/4或25%的观测值。
Q1 = 第一四分位数，或第25百分位数
Q2 = 第二四分位数，或第50百分位数
Q3 = 第三四分位数，或第75百分位数
4.四分位间距：第三四分位数Q3与第一四分位数Q1的差值，也就是中间50%数据的极差。
四分位间距

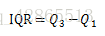
5.z分数：标准化数值，观测值xi与平均数x¯的距离，是zi个标准差。
6.切比雪夫定理：与平均数的距离在z个标准差之内的数据项所占比例至少为(1−1/z2)，其中z是任意大于1的实数。
7.经验法则：
对于具有钟形分布的数据：
大约68%的数据值与平均数的距离在1个标准差之内
大约95%的数据值与平均数的距离在2个标准差之内
几乎所有的数据与平均数的距离在3个标准差之内
8.箱形图：
*上限（最大值）
*（第一四分位数）
*（第二四分位数）
*（第三四分位数）
*下限（最小值）
9.皮尔逊积矩相关系数：

相关系数的范围是-1~+1。当相关系数接近于-1或者+1时，表示强的线性关系，越接近0，线性关系也越弱。相关系数提供了线性但不是因果关系的一个度量，两个变量之间较高的相关系数，并不意味着一个变量的变化会引起另一个变量的变化。