蓝桥杯 算法训练 最大的算式

最大的算式

问题描述
　　题目很简单，给出N个数字，不改变它们的相对位置，在中间加入K个乘号和N-K-1个加号，（括号随便加）使最终结果尽量大。因为乘号和加号一共就是N-1个了，所以恰好每两个相邻数字之间都有一个符号。例如：
　　N=5，K=2，5个数字分别为1、2、3、4、5，可以加成：

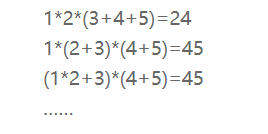
输入格式
　　输入文件共有二行，第一行为两个有空格隔开的整数，表示N和K，其中（2<=N<=15, 0<=K<=N-1）。第二行为 N个用空格隔开的数字（每个数字在0到9之间）。
输出格式
　　输出文件仅一行包含一个整数，表示要求的最大的结果

思路
刚开始动态规划没有什么思路，直接用暴力搜索做的。
思路：将长度为N的数组中相邻的数字依次两两结合，形成N-1个长度为N-1的数组，再对于新的数组进行两两结合形成（N-2)*(N-1）个长度为N-2的数组，依次进行下去，直至数组长度=乘号的数量+1，依次进行判定。

代码

#include <stdio.h>

int ans=0;
int K;
void caculMax(int arr[],int length){
    if(length==K+1){
        int result=1;
        for(int i=1;i<=length;i++){
            result*=arr[i];
            //printf("%d ",arr[i]);
        }
        //printf("\n");
        if(result>ans) ans=result;
        //printf("result=%d\n",result);
    }
    else{
        for(int i=1;i<=length;i++){
            int arrNew[length-1];
            for(int j=1;j<length;j++){
                if(i==j)arrNew[j]=arr[j]+arr[j+1];
                else if(j<i)arrNew[j]=arr[j];
                else arrNew[j]=arr[j+1];
                //printf("%d ",arrNew[j]);
            }
            //printf("\n");
            caculMax(arrNew,length-1);
        }
    }
}
int main(){
    int N;
    int arr[16];
    scanf("%d%d",&N,&K);
    for(int i=1;i<=N;i++){
        scanf("%d",&arr[i]);
    }
    //int nump=N-K-1;
    caculMax(arr,N);
    printf("%d\n",ans);
}

评测结果

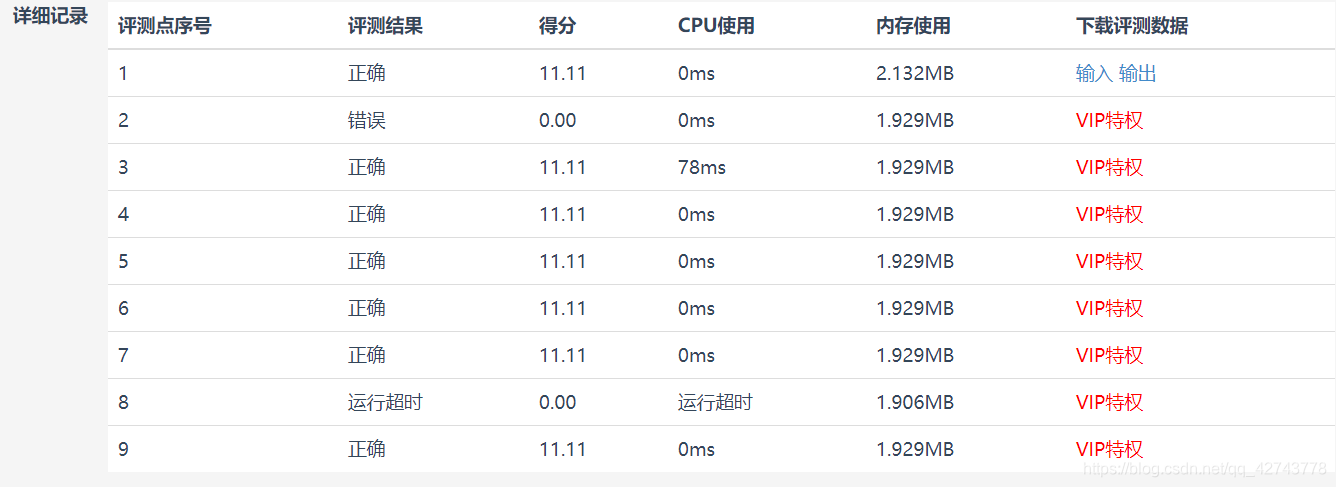
发现能通过大部分测试用例，有一个出现错误，有一个出现运行超时的情况。（后来查询资料发现，运行错误是因为int型溢出了，换成long long型输出就能解决问题）

优化

在穷举（暴力搜索）的过程中发现，当N为15时递归程度太深，时间复杂度过高导致用时直接爆炸。所以暴力搜索只能解决规模较小时的问题。还是踏踏实实走动态规划的路。

动态规划思路：
题目分析：我们用sum[i]保留前i个数的和，用dp[i][j]保留前i个数中含有j个乘号的最大的结果。那么我们最终要求的是dp[N][K]。显然，dp[i][0]=sum[i]，因为没有一个乘号，所以就相当于求前n项和。我们自底向上求解。
这是一个典型的动态规划的问题，首先根据sum[i]可以初始化dp[i][0]，然后一列一列求。先求第二列，j=1的情况。
dp[2][1] = dp[1][0] * num[2] = 2
dp[3][1] = max(dp[2][0]num[3], dp[1][0](num[2]+num[3]))
dp[4][1] = max(dp[3][0]num[4], dp[2][0](num[3]+num[4]), dp[1][0](num[2]+num[3]+num[4]))
所以，我们得到dp[i][j] = max(dp[i][j], dp[p]j-1) (p表示插入的乘号的位置，1<=p<i)*
（以上斜体部分引用自https://blog.youkuaiyun.com/Tesla_meng/article/details/88614520）

思路详解：
对于以上思路并未有严格证明，我认为基础思路是：将多个乘号看成是一个个独立的乘号进行处理，先将乘号数为1时各长度情况下最大值求出来，即dp[i][1],1<i<=N。当乘号数为2时，等价于在乘号1的基础上新增了一个乘号，那么这个乘号可能出现在的位置有p,已有乘号的数量<p<i。以此类推，这样最终dp[N][k]就是所求结果。

代码：

#include <stdio.h>

long long max(long long a,long long b){return a>b?a:b;}
long long K[16][16];
int sum[16];
int arr[16];
int main(){
    int N,k;
    scanf("%d%d",&N,&k);
    for(int i=1;i<=N;i++){
        scanf("%d",&arr[i]);
        if(i!=1)
            sum[i]=sum[i-1]+arr[i];
        else
            sum[i]=arr[i];
    }
    for(int i=0;i<=N;i++){
        for(int j=0;j<i&&j<=k;j++){
            K[i][j]=0;
        }
    }
    K[1][0]=arr[1];
    for(int j=0;j<=k;j++){
        for(int i=2;i<=N;i++){
            if(j==0)K[i][j]=sum[i];
            else{
                for(int w=1;w<i;w++){
                    if(w<=j-1)continue;
                    K[i][j]=max(K[i][j],K[w][j-1]*(sum[i]-sum[w]));
                }
            }
        }
    }
    printf("%lld\n",K[N][k]);
}

代码说明：在我的代码中，dp[i][j]用了K[i][j]进行了表示。（第一版状态转移方程求错了，才看的网上的解析，所以就沿用了原有的K[i][j]的表示。希望不会为您的阅读带来困扰）。其中需要注意的是，w的值不能小于j-1。K[w][j-1]表示的是长度为w的数组中有j-1个乘号，当w<=j-1时，数组中不可能有这么多个乘号，所以是无意义的。（PS：不过不加这个判定，好像也能通过测试）

运行结果：

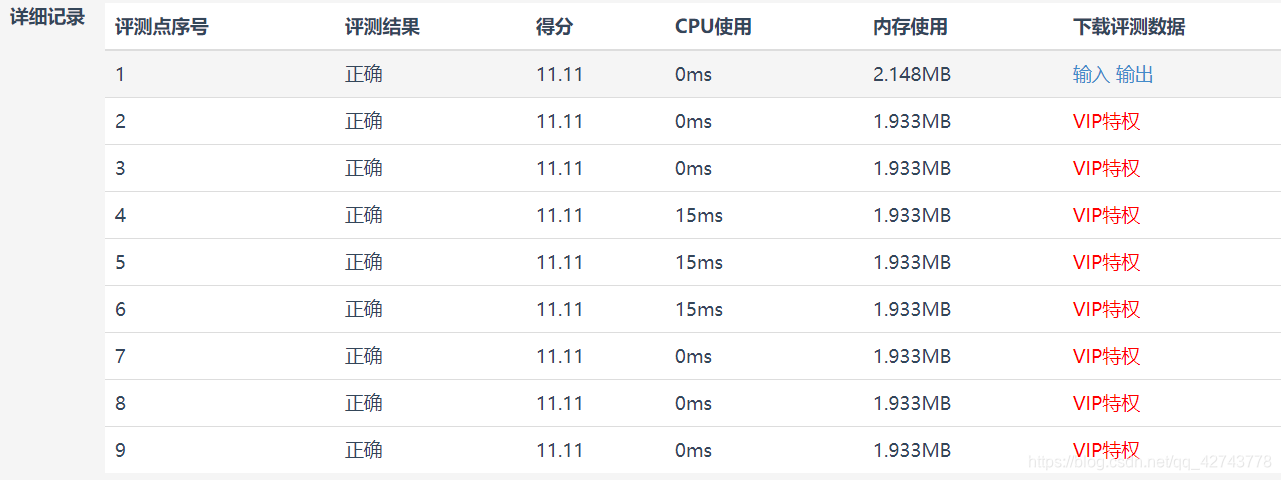
提交记录：

今天也是一只不断学习的小菜鸡啊！
希望我的博客能对您有所帮助，也欢迎留言讨论！