二分

最新推荐文章于 2025-04-26 15:11:06 发布

原创最新推荐文章于 2025-04-26 15:11:06 发布 · 198 阅读

0 ·

CC 4.0 BY-SA版权

杂类同时被 2 个专栏收录

5 篇文章

订阅专栏

二分

1 篇文章

订阅专栏

下面的一些内容来自于《算法竞赛--进阶指南》-李煜（yu第四声）东

二分的基础的用法是在单调序列或单调函数中进行查找。因此当问题的答案具有单调性时，就可以通过二分把求解转化为判定（根据复杂度理论，判定的难度小于求解），这使得二分的运用范围变得很广泛。进一步地，我们还可以扩展到通过三分法去解决单峰函数的极值以及相关问题。

对于整数域上的二分，需要注意终止边界、左右区间取舍时的开闭情况，避免漏掉答案或造成死循环；

对于实数域上的二分，需要注意精度问题。

整数集合上的二分：

在[l,r]以内，循环以l==r结束，每次二分的中间值会归属于左半段和右半段二者之一。

在单调递增序列a中查找>=x的数中最小的一个（即x或x的后继）：

while(l<r){
    int mid = (l+r) >> 1;
    if(a[mid] >= x) r = mid;
    else l = mid + 1;
}
return a[l];

在单调递增序列a中查找<=x的数中最大的一个（即x或x的前驱）：

while(l<r){
    int mid = (l+r) >> 1;
    if(a[mid] <= x) l = mid;
    else r = mid - 1;
}
return a[l];

例题：Best Cow Fences（https://vjudge.net/contest/313348#problem/F）

给定正整数数列A，求一个平均数最大的、长度不小于L的（连续的）子段。

解法：

二分答案，判定“是否存在一个平均数最大的、长度不小于L的（连续的）子段”。

如果把数列中每个数都减去二分的值，，就转发为判定“是否存在一个长度不小于L的子段，子段和非负”。下面我们来着重解决一下两个问题：

1.求一个子段，它的和最大，没有“长度不小于L”这个限制。

无长度限制的最大子段和问题是一个经典问题，只需O（n）扫描该数列，不断把新的数加入子段，当子段和变成负数时，把当前的整个子段清空。扫描过程中出现过的最大子段和即为所求。对这个算法不熟悉的读者建议做To The Max（POJ1050）这道题作为练习。

2.求一个字段，它的和最大，子段的长度不小于L

子段和可以转化为前缀和相减的形式，即设sumi表示A1~Ai的和，则有：

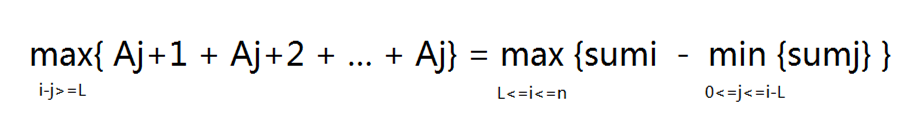
仔细观察上面的式子可以发现，随着i的增长，j的取值范围0~i-L每次只会在增大1.换言之，每次只会有一个新的取值进入min{sumj}的候选集合，所以我们没有必要每次循环枚举j,只需要用一个变量记录当前最小值（min_val），每次与新的取值sumi-L

取min就可以了

解决了问题2之后，我们只需要看一下最大子段和是不是非负数，就可以确定二分上下界的变化范围了。

请读者自己思考使用二分的前提：为什么该问题的答案具有单调性（在上面的图片中可以解答）

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<vector>
#include<map>
#include<set>
#include<queue>
#define rep(i,s,e) for(int i=s;i<=e;i++)
#define rep1(i,s,e) for(int i=s;i<e;i++)
#define rep2(i,s,e,c) for(int i=s;i>=e;i--)
#define pfi(x) printf("%d\n",x)
#define pfl(x) printf("%lld\n",x)
#define pfn() printf("\n")
#define sfi(x) scanf("%d",&x)
#define sfi1(x,y) scanf("%d%d",&x,&y)
#define sff(x) scanf("%lf",&x)
#define sfl(x) scanf("%lld",&x)
using namespace std;
const int MAX = 1e5 + 50;
const int mod = 996873654;
int N,F;
double arr[MAX],b[MAX],sum[MAX];
void init(){
	sfi1(N,F);
	rep(i,1,N){
		sff(arr[i]);
	}
}
int main(){
	init();
	double l=-1e6,r=1e6;//二分答案，即平均数,l和r是平均值最初的取值范围，看题判断 
	double eps=1e-5;//因为l,r是double，所以设置精度eps来判断条件 
	while(r-l>eps){
		double mid = (l+r)/2;//mid就是平均数 
		rep(i,1,N) b[i]=arr[i]-mid;//算出所有数和平均数的差值	
		rep(i,1,N) sum[i]=sum[i-1]+b[i];//算出差值的前缀和 
		double ans=-1e10;
		double min_val = 1e10;
		rep(i,F,N){//枚举右区间为F~N 
			min_val = min(min_val, sum[i-F]);
			ans = max(ans, sum[i]-min_val);//这两步可以算出右区间为i的情况下长度从F~i的最大值 
		}
		if(ans>=0){//如果ans>=0,那么可能还有更优的选择，即更大的平均数 
			l=mid;
		} 
		else r=mid;
	}
	cout<<(int)(r*1000)<<endl;
	return 0;
}