归并排序（也挺快的，0v0）

#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
//对数组a，下标范围在[ns,ne)的元素进行归并排序 
void mergesort(int * array,int ns,int ne)
{
	if(ne-ns==1) //1.递归终止条件，半开区间中只有一个元素，一定有序 
		return;
	//2.二分法，去中间位置
	//对2个子数组进行分开排序
	int m=ns+(ne-ns)/2;//避免溢出，取中间位置
	mergesort(array,ns,m);//左半区间归并排序 
	mergesort(array,m,ne);//右半区间归并排序，包括中值
    if(a[m-1]<a[m]) return;//如果左边最后一个元素小于右边第一个元素，说明已经是顺序的了
	//3.依次取出子数组的元素，合并 
	int *ta=new int[ne-ns];//定义一个临时数组 
	int nl=ns,nr=m;//左右的子数组的下标 
	int nt=0;//临时数组的下标
	while(nl<m&&nr<ne)
	{
		if(array[nl]<array[nr]) {ta[nt]=array[nl];nl++;nt++;}
		else {ta[nt]=array[nr];nr++;nt++;}
	} 
	//若有剩余，必定一个全部取完，另一个有剩余 
	while(nl<m) {ta[nt++]=array[nl++];}
	while(nr<ne) {ta[nt++]=array[nr++];}
	//把临时数组赋值给数组a
	for(int i=0;i<ne-ns;i++)
		array[i+ns]=ta[i];
	//释放临时空间
	delete[] ta; 
}
void print(int array[],int n)
{
	for(int i=0;i<n;i++)
	printf("%d ",array[i]);
}
int main()
{
	int array[]={4,1,10,15,37,79,24,11,91,2,18,94,45,21,52,83,98,90};
	int n=sizeof(array)/sizeof(*array);
	mergesort(array,0,n); 
	print(array,n);
}

迭代版本：

上节的归并排序使用递归的方式实现，递归频繁的调用函数会消耗一定时间，并且对栈的操作也很多，大多数递归算法都可以转化成迭代的方式实现。递归是将数组从上到下的层层分组，减小长度，那么迭代实现的话则是从下到上，设置一个间距，初始为1，则以1为单位进行元素的合并，接下来间距乘以2，以2个元素一组进行合并，重复上述步骤，直至间距大于数组长度。

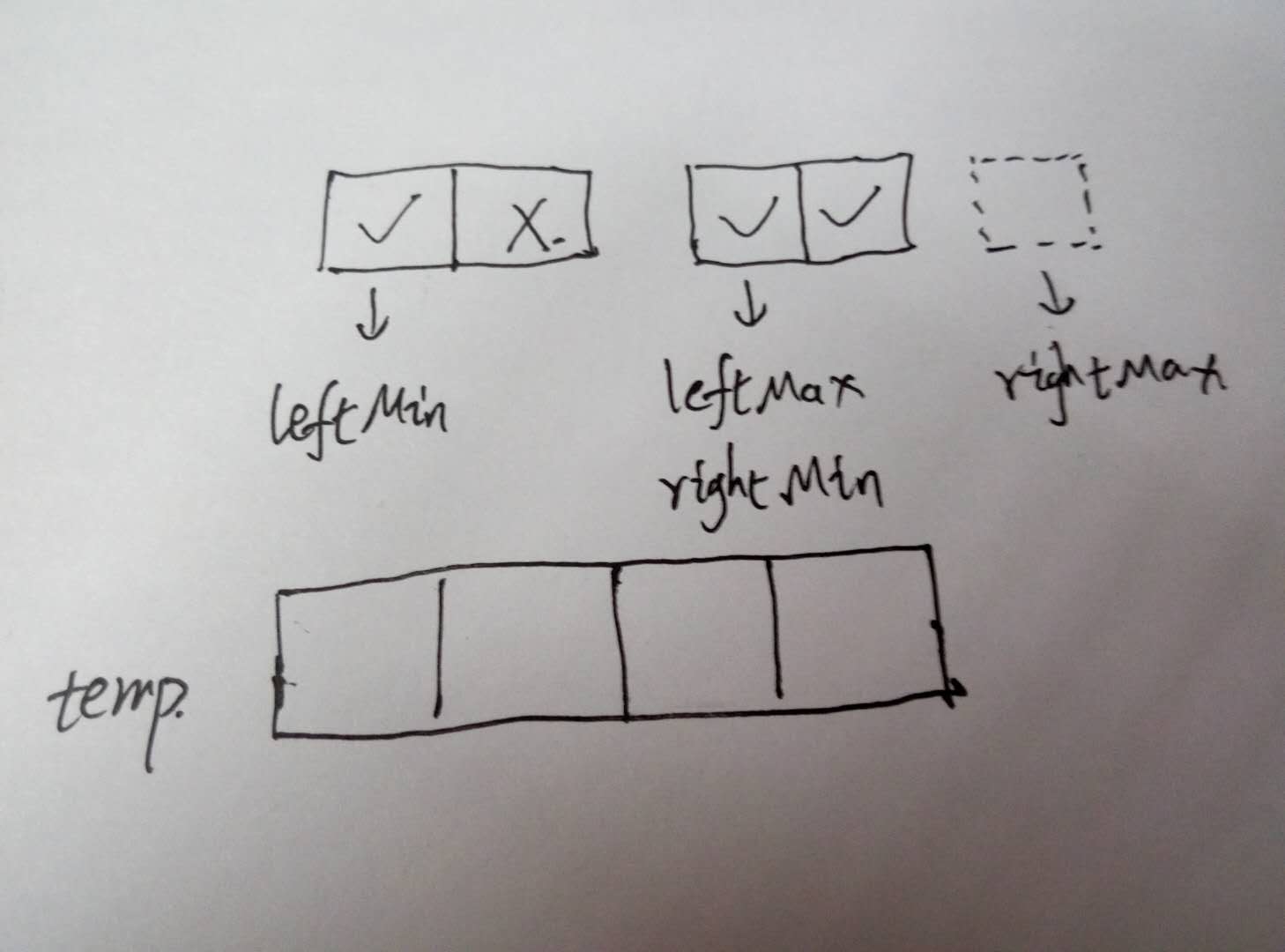
上图以2个元素一组为例，设置4个指针，为

int leftMin, leftMax, rightMin, rightMax
分别指向两组元素的对应位置，当然也可以让leftMax和rightMax分别指向每组的最后一个元素，而不是最后一个元素的下一个位置，合并时需要temp数组，合并过程会出现两个数组中一边先遍历结束的情况：当左边的先遍历结束时，因为右边数组的剩余元素本来就应该待在当前的位置，因此无需处理；当右边的元素先遍历结束时，如图中对勾代表元素已经放到正确的位置，X代表还没有遍历的元素，那么将左边数组未遍历的元素放到右边数组中对应的位置处即可，省去了复制到temp数组再复制回原数组的操作。
--------------------- 
作者：Rap_God 
来源：优快云 
原文：https://blog.youkuaiyun.com/u012936940/article/details/80150017 
版权声明：本文为博主原创文章，转载请附上博文链接！

#include <iostream>
#include <algorithm>
#include <vector>
#define rep1(i,s,e,c) for(int i=s;i<e;i=i+c)
#define rep2(i,s,e,c) for(int i=s;i<=e;i=i+c)
#define rep3(i,e,s,c) for(int i=e;i>=s;i=i-c)
using namespace std;
typedef long long ll;
const int MAX=1e5+1;
const int INF=0x3f3f3f3f;
const int MOD=332748118;
void mergesort(int a[],int n){
	int *t = new int[n];//临时数组t 
	int p=0;//t数组的下标
	//和归并排序递归版本一样，同样是分为两部分
	int leftMin,leftMax,rightMin,rightMax;
	for(int i=1;i<n;i*=2){//i为每部分的长度，每一次翻倍，翻倍后的长度为i的数组已经在翻倍前排完序 
		for(leftMin=0;leftMin<n-i;leftMin=rightMax){//将数组a根据i分成n/i个部分，两两排序 
			//根据leftMin和i确认边界,左闭右开 
			leftMax=leftMin+i;
			rightMin=leftMax;
			rightMax=rightMin+i;
			if(rightMax>n){
				rightMax=n;
			}
			p=0;
			//根据对应下标元素的大小将元素顺序存储到t中 
			while(leftMin<leftMax && rightMin<rightMax){
				a[leftMin]<a[rightMin]?t[p++]=a[leftMin++]:t[p++]=a[rightMin++];
			}
			//如果左边遍历完，右边剩余的部分因为已经最大，不用动 
			//如果右边遍历完，将左边剩余的部分（这部分最大）搬到最右边 
			while(leftMin<leftMax){//右边已经全部遍历完,rightMin在rightMax的位置 
				a[--rightMin]=a[--leftMax];
			}
			while(p>0){
				a[--rightMin]=t[--p];
			}
		}		
	}
	delete[] t; 
}
void print(int a[],int n){
	for(int i=0;i<n;i++){
		cout<<a[i]<<" ";
	}
}
int main()
{
	int n,a[MAX];
	cin>>n;
	for(int i=0;i<n;i++){
		scanf("%d",&a[i]);
	}
	mergesort(a,n);
	print(a,n);
    return 0;
}
/*
8
5 2 7 4 8 1 6 3
*/