数据结构—排序算法总结(插入排序、希尔排序、选择排序、堆排序、冒泡排序、快速排序、合并排序、计数排序)

*排序
所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。
稳定性
在待排序的数组中，如果出现多个相同的关键字，例如：98751555512,中出现重复的数字，在排好序以后，相同数字之间的位置不能发生改变，这种排序算法称为稳定的，否则为不稳定。
排序方法有：插入排序、希尔排序、选择排序、堆排序、冒泡排序、快速排序、合并排序、计数排序，其中计数排序是不需要进行比较的排序
插入排序
插入排序：简单来说，就是把每个元素按照大小，插入到有序数列中。因此，插入排序将带排序列分为两部分，一部分为有序，另一部分无序，就是将无序的元素依次插入到有序部分当中。

void insertionSort(int a[], int size)
{
	//待排序列从i ~ size 
	for (int i = 0; i < size; ++i)
	{
		//将带排序列中第一个元素
		int key = a[i];
		int j;
		// 下标0~j的序列为有序序列，从后往前遍历，如果遇到比无序序列中第一个元素小的，将每个元素后移
		for (j = i - 1; j >= 0 && a[j] > key; --j)  
		{
			a[j + 1] = a[j];
		}
		//将无序元素中的第一个插入到有序序列中
		a[j + 1] = key;
	}
}

希尔排序
例如：9 8 7 6 5 4 3 2 1 中
当gap = 4时 ， 9 与 5进行比较，因为5小所以交换位置，5 与 1进行比较，
当gap = 2时，同理进行比较
当gap = 1时，元素已经有序。

void insertSortWithGap(int a[], int size)
{
	int gap = size / 3 + 1;
	while (gap != 1)
	{
		for (int i = 0; i < size; ++i)
		{
			int key = a[i];
			int j;
			//元素与同它间隔gap个元素比较
			for (j = i - gap; j >= 0 && a[j] > key; j -= gap)
			{
				a[j + gap] = a[j];
			}
			a[j + gap] = key;
		}
		gap = gap / 3 + 1;
	}
}

选择排序
选择排序，就是在一组序列中，选出最小的或者最大的元素，将其让到有序序列中最后一个或者最前一个。

1. 解法一：找出最小值(最大值)，并将其放到有序序列最后面(最前面)。

void selectSort(int a[], int size)
{
	for (int i = 0; i < size; ++i)
	{
		int min = size - 1;
		for (int j = i; j < size; ++j)
		{
			if (a[j] < a[min])
			{
				min = j;
			}
		}
		swap(&a[i], &a[min]);
	}
}

2. 解法二：同时找出最大值与最小值，将最大值放在前面有序序列的最后面，将最大值放在后面有序序列的最前面。
   无序数组 i ~ size - i - 1
   有序数组 0 ~ i 与 size - i -1 ~ size - 1

void selectSort2(int a[],int size)
{
	//因为无序数列   i~size-i-1 
 	for (int i = 0; i < size - i; i++)
	{
		int min = size - 1;
		int max = 0;
		for (int j = i; j < size - i; j++)
		{
			if (a[min] > a[j])
			{
				min = j;
			}
			if (a[max] < a[j])
			{
				max = j;
			}
		}
		//将无序数列中最小的元素，与有序数列中，最后一个元素的下一个位置进行交换
		swap(&a[i], &a[min]);
		//如果无序数列第一个数就是其最大元素，因为上面将其位置进行交换了，所以最大元素的地址就为之前的最小元素的位置
		if (max == i)
		{
			max = min;
		}
		swap(&a[max], &a[size - i - 1]);
	}
}

快速排序
快速排序就是找一个基准值，将比基准值小的放在左边，比基准值大的放在右边，就将待排序列分为两部分，一部分是比基准值小的，一部分是比基准值大的，最后在对左右两部分重复上面的方法，直到数组有序。
在一次遍历以后，左边全都为小于基准值的，右边全为大于基准值的。

int Quick_Sort(int a[], int left, int right)
{
	int begin = left;
	int end = right;
	int key = a[right];

	while (begin < end)
	{
		while (begin < end&&a[begin] <= key)
		{
			begin++;
		}
		while (begin<end&&a[end]>= key)
		{
			end--;
		}
		swap(&a[begin], &a[end]);
	}
	swap(a + begin, a + right);
	return begin;
}

void quickSort(int a[], int left, int right)  
{
	if (left >= right)
	{
		return;
	}
	int i = Quick_Sort(a, left, right - 1);
	quickSort(a, left, i);
	quickSort(a, i + 1, right);
}

堆排序
堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆，排降序建小堆。

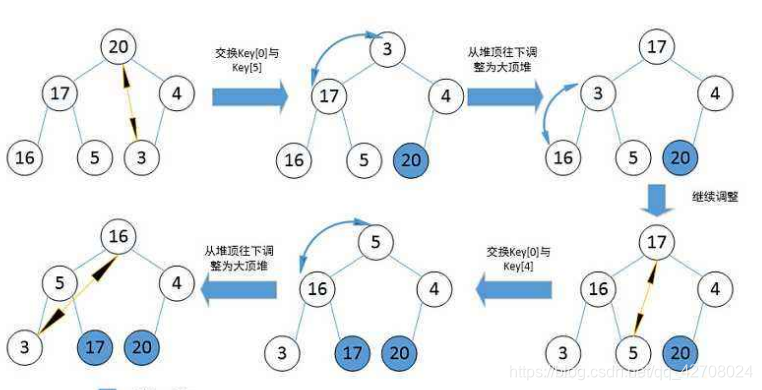
• 创建堆

按照下标的形式进行建堆

void createHeap(int a[], int size)
{
	for (int i = (size - 2) / 2; i >= 0; --i)
	{
		heapify(a, size, i);
	}
}

//建小堆(双亲结点的值比左右孩子结点的值都小)

void heapify(int a[], int size, int i)
{
	int left = i * 2 + 1;
	int right = i * 2 + 2;
	if (left >= size)
	{
		return;
	}
	int min = left;
	if (right < size && a[right] < a[min])
	{
		min = right;
	}
	if (a[i] < a[min])
	{
		return;
	}
	swap(a[i], a[min]);
	heapify(a, size, min);//不断进行向下调整
}

//建大堆

void  heapitf(int a[], int size, int index)//建大堆，降序排列
{
	int left = index * 2 + 1;
	int right = index * 2 + 2;
	if (left >= size)
	{
		return;
	}
	int max = left;
	if (right < size && a[right] >a[left])
	{
		max = right;
	}
	if (a[index] >= a[max])
	{
		return;
	}
	int temp = a[max];
	a[max] = a[index];
	a[index] = temp;
	
	heapitf(a, size, max);
}

运行结果：

归并排序
归并排序，运用分治法的思想，将问题规模不断进行缩减，最终将所有的结果进行合并就得出原问题的解。在排序中，例如：8 7 6 5 4 3 2 1这一串数字进行排序，先将问题分为8 7 6 5一组 4 3 2 1 一组进行排序，如果还无法排序就进一步将问题进行划分，最终再将排好序的元素进行整合。

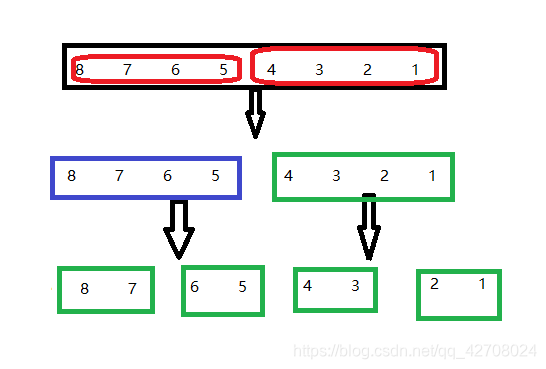
void Merge(int *a, int left, int mid, int right)
{
	int *temp = (int *)malloc(sizeof(int)*(right - left));
	int index = 0;
	int l = left;
	int m = mid + 1;
	while (l <= mid&&m <= right)
	{
		if (a[l] <= a[m])
		{
			temp[index++] = a[l++];
		}
		else
		{
			temp[index++] = a[m++];
		}
	}
	while (l <= mid)
	{
		temp[index++] = a[l++];
	}
	while (m <= right)
	{
		temp[index++] = a[m++];
	}
	for (int i = 0, j = left; j <= right; ++j)
	{
		a[j] = temp[i++];
	}
}

void Mergesort(int* a, int left, int right)
{
	if (left >= right)
		return;
	int mid = left + ((right - left) >> 1);
	Mergesort(a, left, mid);
	Mergesort(a, mid + 1, right);
	Merge(a, left, mid, right);

计数排序

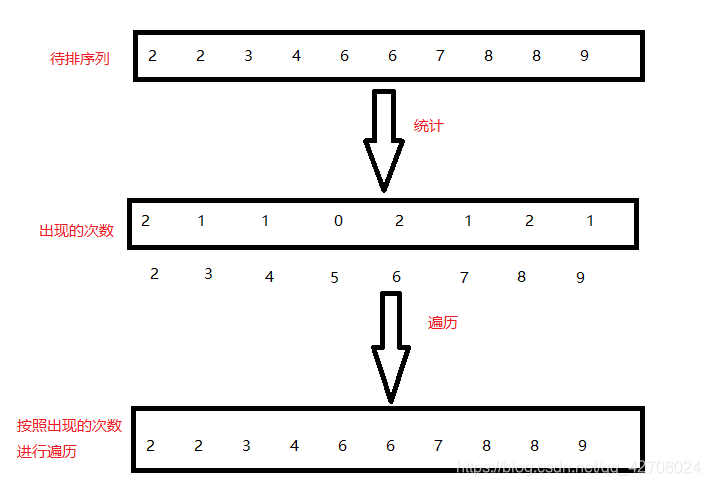
void CountSort(int *a, int size)
{
	int min = a[0];
	int max = a[0];
	int index = 0;
	for (int i = 0; i < size; ++i)
	{
		if (a[i] < min)
		{
			min = a[i];
		}
		if (a[i] > max)
		{
			max = a[i];
		}
	}
	int range = max - min + 1;
	int *temp = (int*)calloc(range, sizeof(int));
	for (int i = 0; i < size; ++i)
	{
		temp[a[i] - min]++;
	}
	for (int i = 0; i < range; i++)
	{
		while (temp[i]--)
		{
			a[index++] = i + min;
		}
	}
	free(temp);
	temp = NULL;
}

堆排序代码
先创建大顶堆，在不断进行调整

void adjust(vector<int>& arr, int index, int size)
{
	int left = index * 2 + 1;
	int right = index * 2 + 2;
	int max = index;
	if (left<size && arr[left]>arr[max])
		max = left;
	if (right<size && arr[right] >arr[max])
		max = right;

	if (max != index)
	{
		swap(arr[max], arr[index]);
		adjust(arr, max, size);
	}
	
}

//对大顶堆进行不断调整
void heapSort(vector<int>& arr, int size)
{
	for (int i = size / 2 - 1; i >= 0; --i)
	{
		adjust(arr, i, size);
	}
	for (int i = size - 1; i >= 0;i--)
	{
		swap(arr[0], arr[i]);
		adjust(arr,0,i);
	}
	for (int i = 0; i < size; ++i)
		cout << arr[i] << " ";
}