【蓝桥杯备战】递推、递归、前缀和、差分

原创

于 2020-07-16 21:15:35 发布 · 391 阅读

1 ·

CC 4.0 BY-SA版权

本文深入探讨了在解决洛谷P1255数楼梯问题时使用高精度运算的方法，以及如何通过递归来解决计蒜客T2116选数问题，寻找素数和的有效组合。

首先是递推，洛谷P1255 数楼梯。
阶梯思路如图：
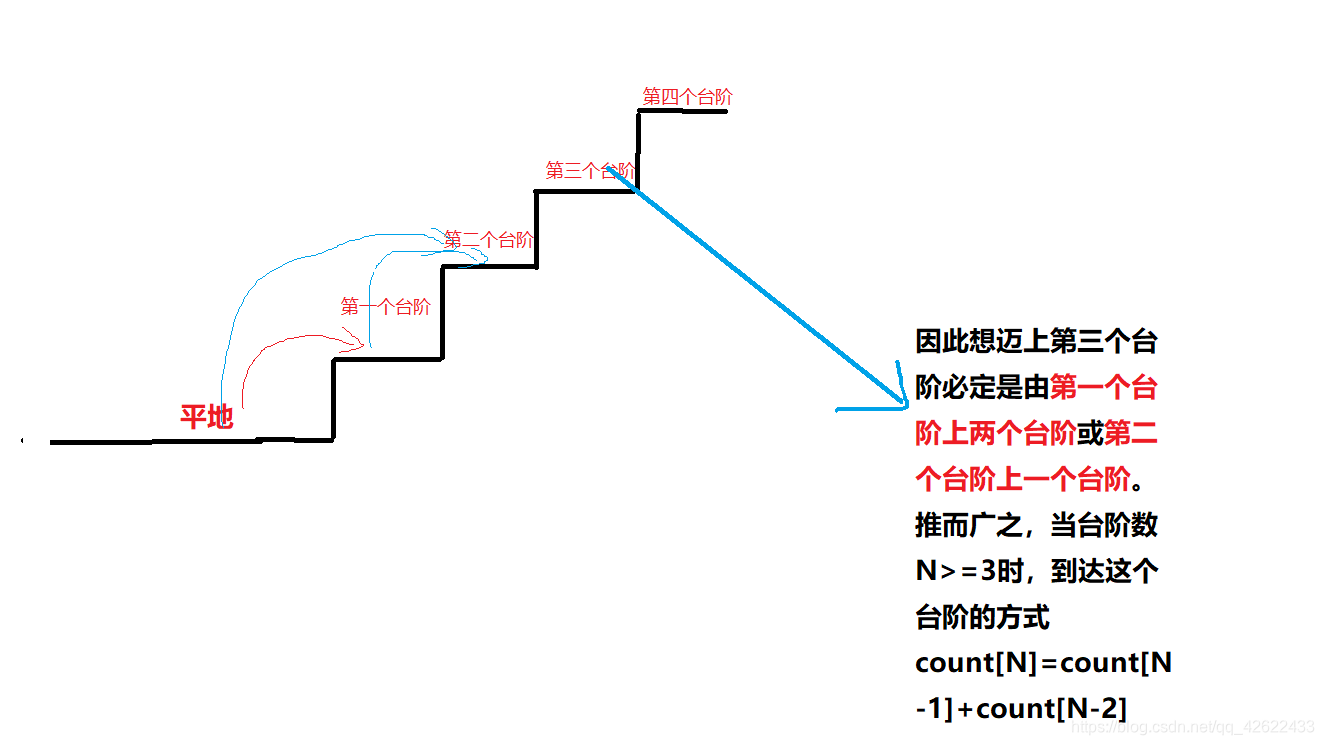
在这里插入图片描述
但是由于该题N最大能到5000，显然，数值过大会爆掉long long，因此我们需要自己定义个数组自己模拟加法运算，被称为高精度运算。
这里先上代码，然后上模拟这个运算过程的图。

#include <iostream>
#include <cstring>
#include <vector> 
#include <cstdio>
using namespace std;
//台阶最大数为5000，我们定义个5005
const int STEP_MAX=5005;
//定义一个二维数组作为表格。tab[n]表示上第n个台阶的方式数量
int tab[STEP_MAX][STEP_MAX];
//len表示当前方法数的位数
int len=1;
void jump(int k){
   
   
	//将前面两个台阶的方法数每位相加
	for(int i=1;i<=len;i++){
   
   
		tab[k][i]=tab[k-1][i]+tab[k-2][i];
	}
	//进位
	for(int i=1;i<=len;i++){
   
   
		if(tab[k][i]>=10){
   
   
			tab[k][i+1]+=tab[k][i]/10;
			tab[k]