HDU2879-HeHe(积性函数)

最新推荐文章于 2020-01-13 09:21:46 发布

原创最新推荐文章于 2020-01-13 09:21:46 发布 · 262 阅读

1 ·

CC 4.0 BY-SA版权

数学==杜教筛/莫比乌斯/积性函数/欧拉等数论专栏收录该内容

32 篇文章

订阅专栏

本文探讨了He函数的定义及其在求解特定方程解数中的应用。He函数被证明是一个积性函数，通过分解质因数可以高效计算其值。文章提供了计算He函数值的算法，并使用实例说明了如何求解HeHe[n]%m的值。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目
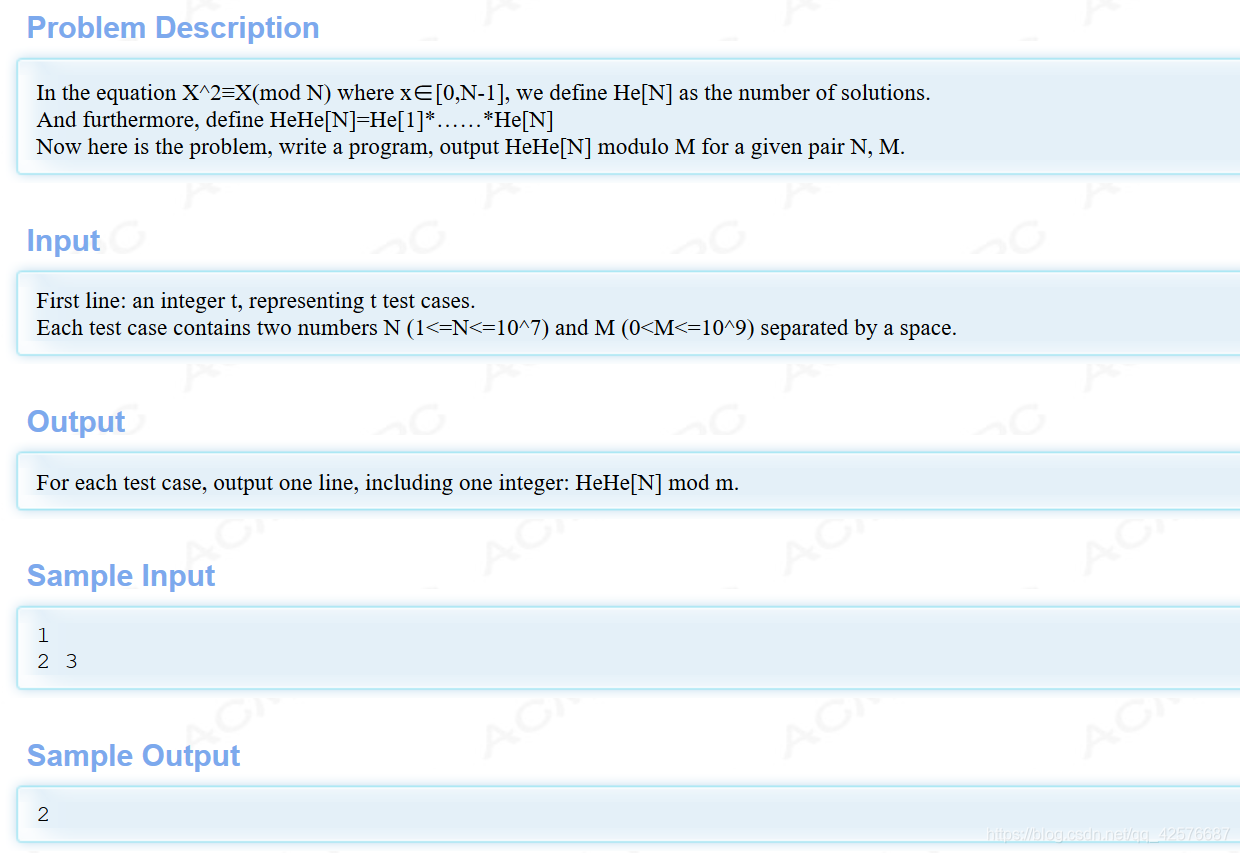
在这里插入图片描述
题意：He[N]的值为方程(X^2)%N=X解的个数. HeHe[N]是He[N]的前缀积.
多组样例n,m：求HeHe[n]%m的值.
题解:像这种只给个公式的,一般是打表或者积性函数。打表没看出来规律。

证明He[n]是积性函数: 分步证明:
1.p是质数:He[p]=2。(x=0,x=1)
2.gcd(a,b)=1,He[a*b]=He[a]He[b];
证出除0,1以外的两组解习，证明每一组解系分别只有一个满足题意，x1,x2.
证明x1!=x2；
3.He[p^k]=2;(p为质数时)；

He[300]=He[2^2 * 3 * 5^2 ]=He[2^2] he[3] *He[5^2]= 2 * 2 * 2；
p有x个质因子则He[p]=2^x；
计算He[p] * He[p-1] * He[p-1] * … * He[1]的话看代码。。很简单的

#include<cstdio>
#include<cmath>
#include<iostream>
#include<algorithm>
#define en '\n'
using namespace std;
typedef long long ll;
const int N=1e7+5;
int prime[N/7],is[N],tot;
void getprime()
{
    for(int i=2;i<=N-5;++i)
    {
        if(!is[i]) prime[++tot]=i;
        for(int j=1;j<=tot&&(ll)i*prime[j]<=N-5;++j)
        {
            is[i*prime[j]]=1;
            if(i%prime[j]==0) break;
        }
    }
}
ll quick_pow(ll c,ll p,ll mod)
{
    ll res=1;
    while(p)
    {
        if(p&1) res=res*c%mod;
        c=c*c%mod;
        p>>=1;
    }
    return res;
}
int main()
{
    getprime();
    int T;scanf("%d",&T);
    while(T--)
    {
        int n;ll mod;scanf("%d%lld",&n,&mod);
        ll ans=0;
        for(int i=1;prime[i]<=n&&i<=tot;++i)
            ans+=n/prime[i];//!!!
        printf("%lld\n",quick_pow(2,ans,mod));
    }
}