最简单的搜索算法

目前自己用的比较多的是广搜bfs
以下是别的大神们的详细讲解：

原网址：https://blog.youkuaiyun.com/a8082649/article/details/81395359
BFS可用于解决2类问题：

从A出发是否存在到达B的路径；
从A出发到达B的最短路径(这个应该叫最少步骤合理)；
其思路为从图上一个节点出发，访问先访问其直接相连的子节点，若子节点不符合，再问其子节点的子节点，按级别顺序依次访问，直到访问到目标节点。

所谓的"图"为: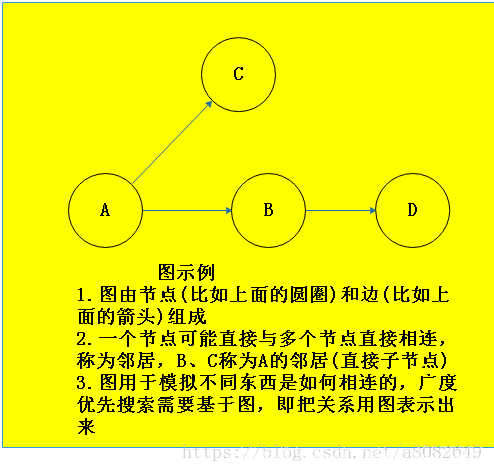
案例

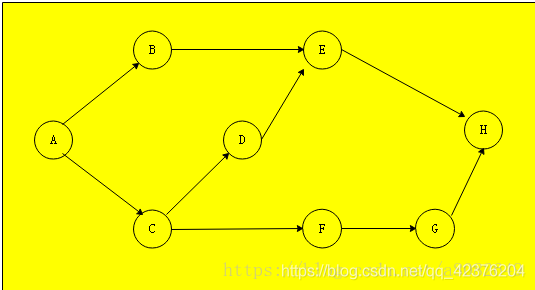
如上图所示，找出从A到H的最短路径(步骤最少的，假设每一段距离相等),此时就可以使用广域搜索算法，原理步骤为:

假设存在一个空的搜索队列Queue,首先将节点A添加进队列Queue
判断队列第一个节点是否是需要查找的目标节点，若不是，则将第一个节点的直接子节点添加进队列，并移除第一个节点
重复判断，直到第一个节点为目标节点，或者队列为空(即代表没有合适的)
如下图所示:

过滤已经搜索过的节点

对于已经搜索过的节点，最好将其唯一的id标识保存下来，后续搜索过程中如果再次出现该节点则跳过不再重复搜索，以提高效率和避免死循环；

举个例子：
imustACM 2025
题目描述
小明听说机场是一个很肥的地方，所以想跳一波机场，看看到底有多肥。不过机场虽然肥，但是跳的人也多。小明第一次跳机场，刚跳下来就到处都是枪声，小明吓得快要哭出来了，想逃离机场，emmm，还是打野比较适合他。
现在把机场看作一个二维平面，’.’代表可以走的空地，’@’代表小明当前的位置，’x’代表这里是个障碍物，’o’代表这里有个敌人，并且手里有枪，敌人可以攻击上下左右四个方向，小明只要走到或者一开始就在敌人可以攻击的位置，就会死亡（机场个个都是98K爆头dalao），子弹不会穿过障碍物，敌人不会移动。小明只能往上下左右走，每走一步需要1秒，只要小明移动到机场的边缘再走一步就算逃离了机场，现在小明请你帮他找一条最快逃离机场的线路，输出这个时间，如果怎么都逃不出去，输出“no zuo no die!”（不含引号）。

输入
多组测试数据，首先第一行一个整数T，代表测试数据组数。1 ≤ T ≤ 100。
每组测试数据有n，m（1 ≤ n，m ≤ 200），代表机场是一个n×m的方阵，接下来是一个由’.’，’@’，’x’，’o’ 构成的n×m的方阵，’@’只有一个。

输出
对于每组数据输出一个数代表最快需要多少时间逃出机场，或者“no zuo no die!”。

样例输入

3
5 5
.x.x.
.x.x.
…
…@…
.o.o.
3 3
@…
xxx
o.x
3 3
o.o
.@.
.x.

样例输出

4
1
no zuo no die!

解题思路：既然士兵o可以狙击，那我们直接把他可以狙击的地方都定义成
'!'表示这是他可以狙击到的地方，为什么不定义成墙壁’x’呢？刚开始我就是定义成这个的，结果浪费了我好多时间，一直WA（痛哭）。因为把狙击的地方定义成墙壁就无法判断原本真正的墙壁！（因为题目所言子弹是无法穿过墙壁的，写的时候如果把假墙壁判断了就不能穿过了~）

解题代码：

#include <iostream>
#include <string>
#include <algorithm>
#include <stack>
#include <stdio.h>
#include <vector>
#include <math.h>
#include <queue>
#include <list>
#include <cstring>
using namespace std;
char maps[300][300];
int mark[300][300];
int dir[4][2] = { {1,0},{0,1},{-1,0},{0,-1} };
int n, m;

struct node
{
    int x;
    int y;
    int step;
    friend bool operator<(const node &a,const node &b)//重载.....具体为啥到现在也不懂。。。
    {
        return a.step > b.step;
    }
};
bool mark1 = true;
void letgo(int x,int y)
{
    mark1 = true;
    maps[x][y] = '!';//这一步很重要！这是子弹的路径
    for(int k = 0;k < 4;k++)//这两个for循环可以减少通多代码量的（自我感觉）
    {
        int x1 = x, y1 = y;
        for(int i = 0;i < 200;i++)
        {
            x1 += dir[k][0];
            y1 += dir[k][1];

            if(maps[x1][y1] == 'x' || maps[x1][y1] == 'o' || x1 < 0 || x1 >= n || y1 < 0 || y1 >= m)//这一步也很重要如果不break就会产生数组越界。。会报Runtime Error
                break;
            if(maps[x1][y1] == '@')//既然一开始就能狙击，那小明无路可走
            {
                mark1 = false;
                break;
            }
            if(maps[x1][y1] == '.')
                maps[x1][y1] = '!';//都没发现异常，就直接定义成狙击路径啦
        }
    }
}

int bfs(int x,int y)
{
    memset(mark,1,sizeof(mark));//mark数组是判断有没有走过这条路的，防止重复走
    priority_queue<node>ming;
    ming.push({x,y,0});
    mark[x][y] = 0;
    while(!ming.empty())
    {
        node go = ming.top();
        ming.pop();//既然弹出来判断了，这一个点就直接不要了

        if(go.x == n - 1 || go.y == m - 1 || go.x == 0 || go.y == 0)
            return go.step + 1;

        for(int k = 0;k < 4;k++)
        {
            int x1 = go.x + dir[k][0];
            int y1 = go.y + dir[k][1];

            if(x1 >= 0 && x1 < n && y1 >= 0 && y1 < m && maps[x1][y1] != 'x' && mark[x1][y1] && maps[x1][y1] != '!')
            {
                ming.push({x1,y1,go.step + 1});//没发现异常就步数+1
                mark[x1][y1] = 0;
            }
        }

    }
    return -1;
}

int main()
{
    int t;
    cin >> t;
    while(t--)
    {
        cin >> n >> m;
        mark1 = true;
        int x, y;
        for(int k = 0;k < n;k++)
        {
            for(int h = 0;h < m;h++)
            {
                cin >> maps[k][h];
                if(maps[k][h] == '@')
                {
                    x = k;
                    y = h;
                }
            }
        }
        for(int k = 0;k < n;k++)
        {
            for(int h = 0;h < m;h++)
            {
                if(maps[k][h] == 'o')
                {
                    letgo(k,h);//找到狙击手就遍历其狙击范围
                    if(!mark1)
                    {
                        cout << "no zuo no die!" << endl;
                        break;
                    }
                }
            }
           if(!mark1)
            break;
        }
        if(!mark1)
            continue;
        int i = bfs(x,y);
        if(i != -1)
            cout << i << endl;
        else
            cout << "no zuo no die!" << endl;
    }

    return 0;
}