机器学习实战之 -- NaiveBayes

NaiveBayes

一、工作原理

1.条件概率：

$$P(X=x|Y=c_k)=P(X^{(1)}=x^{(1)},...,X^{(n)}=x^{(n)}|Y=c_k),k=1,2,3,...,K$$

2.朴素贝叶斯成立的条件概率假设：

$$\begin{gathered} P(X=x|Y=c_k)=P(X^{(1)}=x^{(1)},...,X^{(n)}=x^{(n)}|Y=c_k) \\ =\prod _{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_k) \end{gathered}$$

3.后验概率：

$$\begin{gathered} P(Y=c_k|X=x)=\frac{P(X,Y)}{P(X)} \\ =\frac{P(X=x|Y=c_k)P(Y=c_k)}{{\sum }_{k}P(X=x|Y=c_k)P(Y=c_k)},k=1,2,3,...,K \end{gathered}$$

3.朴素贝叶斯分类器：

$$y=f(x)=arg\underset{c_k}{\max }\frac{P(Y=c_k){\prod }_{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_k)}{{\sum }_{k}P(X=x|Y=c_k)P(Y=c_k)},k=1,2,3,...,K$$
注意到，上式中分母对所有的$c_k$都是相同的，所以，
$$y=f(x)=arg\underset{c_k}{\max }P(Y=c_k)\prod _{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_k),k=1,2,3,...,K$$

二、核心代码

from numpy import *

def loadDataSet():
    '''
    Desc：创建实验样本
    '''
    postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                 ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                 ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                 ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                 ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                 ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0,1,0,1,0,1]    #1 侮辱性, 0 正常
    return postingList,classVec

def createVocabList(dataSet):
    '''
    Desc：处理dataset返回不重复词表
    '''
    #创建一个空集合
    vocabSet = set([])  
    for document in dataSet:
        # 用于求两个集合的并集
        vocabSet = vocabSet | set(document)
    return list(vocabSet)
# 
def setOfWords2Vec(vocabList, inputSet):
    '''
    Desc：词集模型，构造词向量
    vocabList：词库
    inputSet：待转换词
    '''
    # 创建一个与词汇表等长的向量，所有元素都为0
    returnVec = [0]*len(vocabList)
    # 遍历输入文档中的每个词
    for word in inputSet:
        # 判断词是否在词汇表中
        if word in vocabList:
            # 将词在词汇表中出现的位置，对应的标记在等长0向量中
            returnVec[vocabList.index(word)] = 1
        else: print("the word: %s is not in my Vocabulary!" % word)
    return returnVec

# 
def trainNB0(trainMatrix,trainCategory):
    '''
    Desc：朴素贝叶斯分类器训练函数
    params:
            trainMatrix:文档矩阵
            trainCategory:标签向量
    return:
            
        
    '''
    # 文档行数（向量个数）
    numTrainDocs = len(trainMatrix)
    # 词的个数
    numWords = len(trainMatrix[0])
    # 计算侮辱性文字的先验概率：P(y=1)
    pAbusive = sum(trainCategory)/float(numTrainDocs)
    # 构造两个与词汇表相同长度的向量，元素均为1，避免算多个概率的乘积为0。
    p0Num = ones(numWords); p1Num = ones(numWords)      #change to ones() 
    p0Denom = 2.0; p1Denom = 2.0                        #change to 2.0
    # 遍历所有的向量
    for i in range(numTrainDocs):
        # 如果是侮辱性文字
        if trainCategory[i] == 1:
            # 统计侮辱性词出现的频率
            p1Num += trainMatrix[i]
            print(trainMatrix[i],'trainMatrix[i]====')
            print(p1Denom,'before====p1Denom')
            # 统计行中所有词数
            p1Denom += sum(trainMatrix[i])
            print(p1Denom,'p1Denom====')
        else:
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    # 太多很小的数相乘，避免下溢出或者浮点数舍入导致的错误
    p1Vect = log(p1Num/p1Denom)          #change to log()
    p0Vect = log(p0Num/p0Denom)          #change to log()
    return p0Vect,p1Vect,pAbusive

listPosts,listClasses = loadDataSet()
myVocaList = createVocabList(listPosts)
trainMat = []
for postinDoc in listPosts:
    trainMat.append(setOfWords2Vec(myVocaList,postinDoc))
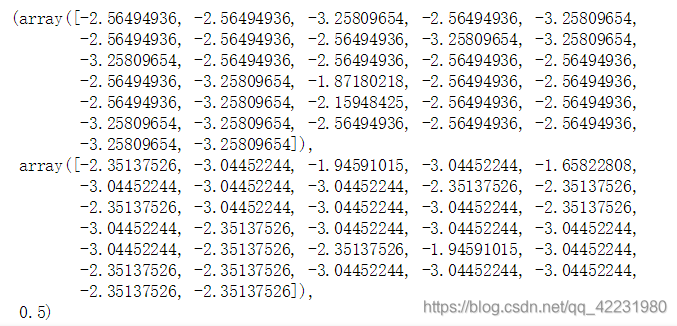
p0v,p1v,pAb = trainNB0(trainMat, listClasses)
p0v,p1v,pAb

def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
    '''
    Desc：计算后验概率分类
    vec2Classify：词向量
    p0Vec：类别为0的条件概率
    p1Vec：类别为1的条件概率
    pClass1：类别为1的先验概率
    '''
    # 已知p1求后验概率
    p1 = sum(vec2Classify * p1Vec) + log(pClass1)    #element-wise mult
    # 已知p0求后验概率
    p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)
    # 分类
    if p1 > p0:
        return 1
    else: 
        return 0
        
def testingNB():
    '''
    Desc：测试算法
    '''
    listOPosts,listClasses = loadDataSet()
    myVocabList = createVocabList(listOPosts)
    trainMat=[]
    for postinDoc in listOPosts:
        trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
    p0V,p1V,pAb = trainNB0(array(trainMat),array(listClasses))
    testEntry = ['love', 'my', 'dalmation']
    thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
    print(testEntry,'classified as: ',classifyNB(thisDoc,p0V,p1V,pAb))
    testEntry = ['stupid', 'garbage']
    thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
    print(testEntry,'classified as: ',classifyNB(thisDoc,p0V,p1V,pAb))

testingNB()

[‘love’, ‘my’, ‘dalmation’] classified as: 0
[‘stupid’, ‘garbage’] classified as: 1

持续更新中…