输出一个标量

接着上篇概述,我们来使用宝可梦进行回归的例子


- 首先函数的样子就是,输入进化前的梦可宝的cp值,输出进化后的cp值
- 之后我们规定线性方程范围,图中颜色深浅
- 我们使用
l
o
s
s
=
∑
(
正
确
c
p
值
−
函
数
估
计
c
p
值
)
2
loss=\sum(正确cp值-函数估计cp值) ^{2}
loss=∑(正确cp值−函数估计cp值)2 90图中颜色代表
4.随机取初始值,计算偏微分,更新w,b参数,不断是loss最小( 图中颜色越好loss越大,越蓝loss越小 )

如果损失函数的方程式这样的,那么能不能达到全局最低点,是要靠人品的,就像上面的两个红线不同的结果
10只宝可梦利用线代知识就能解出理想的线性方程,那为什么还要用梯度下降?因为梯度下降不管是什么函数,只要参数是可微的,都可以帮助我们找到理想的函数,当然我们可以穷举所有的参数,找到好的方程,但是这种做法是不理想的,那么梯度下降是什么思路呢?假设损失函数就w一个参数
- 随机或者有意选取初始点w0
- 计算w梯度(梯度是矢量,方向指向方向导数最大的方向,大小就是最大的方向导数),之后我们减去梯度就能得到理想的局部最小或者是全局最小点,为什么是减号呢?因为梯度带方向也就是带正负号,假如下降阶段,我们就要往正方向走才能到小的点,梯度是负的,那么两个减号变加号,w值就会增加,往正方向走;同理在上升阶段。
η
\eta
η 则决定了你前进或者回退的速度(线性回归不会遇到局部最小的问题)

关于函数选取的tips
函数虽然越复杂,训练集合可能loss就越低,但是到了测试集可能loss会越高这就是过拟合

改进模型
其实上面的数据太少了,根本代表不了梦可宝的cp值,我们需要根据不同的物种设计不同的函数

改进函数如下
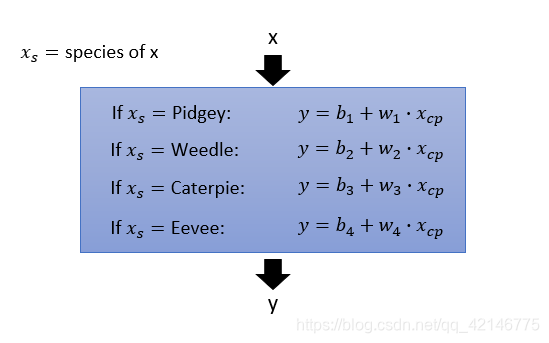
并且我们可以将if结果改造成不带if的线性模型

当然模型还是不够的,比如还有其他的影响值(体重)
改进loss(regularization)
loss只考虑的预测值,regularization还考虑的权值,参数越接近0越好,loss越小,为什么要接近0呢?因为参数越小越平滑,平滑就是输入有变化,输出对输入变化不敏感,为什么不敏感呢?因为
Δ
x
i
\Delta x_i
Δxi代表输入变换,
w
i
w_{i}
wi越小,
w
i
Δ
x
i
w_{i}\Delta x_i
wiΔxi越小,为什么我们喜欢平滑的函数?因为如果我们输入具有噪声干扰,那么干扰就越小。
但是也要注意我们也不喜欢太平滑的函数,所以我们需要调整
λ
\lambda
λ 来调整平滑程度

regularization时不考虑bias,因为调整bias只是在将函数上下平移,不改变平滑程度

























 4146
4146

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










